Анализ работы цепей управления и построение простой модели малого сигнала повышающе-понижающего конвертора с помощью алгебраического подхода
Сегодня известно большое количество ШИМ-преобразователей (конвертеров), используемых в разных технологических установках, в которых выходной сигнал контролируется прямым выбором коэффициента заполнения (коэффициента рабочего цикла) d(t). В связи с этим была введена и получена функция передачи малого сигнала, связывающая форму сигнала выходного напряжения конвертера с коэффициентом заполнения [1–3].
Другой, также широко распространенный подход управления — это текущий программируемый контроль (ТПК) [3, 4], где выходной сигнал преобразователя управляется выбором пикового значения переключаемого тока силового транзистора is(t). Управляющий входной сигнал представляет собой контрольный ток iC(t) (контрольный сигнал), при этом управляющий транзистор включает и выключает сеть так, что пиковый ток транзистора следует за током iC(t)(рис. 1).

Рис. 1. Управляющий (контрольный) входной сигнал iC(t) и ток переключения is(t)
Рабочий цикл транзистора (коэффициент заполнения d(t)) напрямую не контролируется, но зависит от управляющего входного сигнала тока iC(t), тока индуктора iL(t), напряжения конденсатора и входного питающего напряжения. В этих преобразователях осуществляется непрерывный контроль тока силового ключа, то есть преобразователи работают в режиме текущего контроля (ТК).
Структура преобразователя, действующего в режиме ТК, показана на рис. 2. Импульс синхронизации на вход S триггера инициирует период переключения и переводит выход триггера Q на высокий уровень, активируя силовой транзистор. Пока транзистор открыт, ток переключения is(t) равен току через индуктивный дроссель L(is(t) = iL(t)), этот ток возрастает с некоторым положительным наклоном с коэффициентом m1, который зависит от величины индуктивности и напряжения питания преобразователя. В более сложных преобразователях ток is(t) может равняться суммарному току нескольких индукторов.

Рис. 2. Блок-схема преобразователя, работающего в режиме текущего контроля тока
В итоге ток переключения транзисторного ключа приравнивается к току контроля iC(t), и в момент равенства обоих токов происходит переключение транзисторного ключа в закрытое состояние, в течение остальной части периода ток индуктора L снижается. Сигнал переключения формируется в контроллере за счет сравнения токов is(t) и iC(t) (как правило, на вход компаратора подаются сигналы в виде напряжения, пропорциональные данным токам, коэффициент пропорциональности равен значению сопротивления Rf), для этого используется компаратор, чей выходной сигнал подается на R-вход триггера. В результате при is(t) ≥ iC(t) выход триггера из высокого состояния переходит в низкое, что способствует закрыванию ключа.
Как правило, контур обратной связи предназначен для регулирования выходного напряжения v(t), которое сравнивается с задающим напряжением vзад(t) для генерирования сигнала ошибки. Этот сигнал подается на вход компенсационного блока, чей выходной сигнал iC(t)Rf подается на инверсный вход аналогового компаратора.
Для того чтобы создать такую систему обратной связи, необходимо смоделировать влияние изменения тока iC(t) и входного напряжения vg(t) на выходное напряжение v(t). Главным преимуществом данного способа управления является его более простая динамика. Для системы первого порядка передаточная функция по малому сигналу ![]() /
/![]() содержит на один полюс меньше, чем передаточная функция
содержит на один полюс меньше, чем передаточная функция ![]() /
/![]() . Обычно частота, соответствующая этому полюсу, смещена на сторону более высокой частоты и приближена к частоте переключения преобразователя [2, 3].
. Обычно частота, соответствующая этому полюсу, смещена на сторону более высокой частоты и приближена к частоте переключения преобразователя [2, 3].
Впрочем, обычно можно получить простое и надежное управление выходным напряжением в широком диапазоне частот, без использования цепи компенсатора. Естественно, что необходимо иметь схему для измерения текущего значения тока переключения iS(t), однако для такой схемы понадобится система управления с регулируемым коэффициентом заполнения для защиты силового транзистора от чрезмерного тока во время переходных процессов и при условии отказа работы схемы. Очевидно, что программированное управление при снижении текущего значения тока позволяет предотвратить большие потери в транзисторе с помощью ограничения максимального значения тока iC(t) и получить при этом более простую динамику системы. СУ с текущим контролем тока обеспечивает гарантированное отключение силового транзистора, когда в течение рабочих циклов ток переключения становится слишком большим [2, 3, 5].
Дополнительным преимуществом в полной мостовой схеме и двухтактных изолированных преобразователях является сокращение или устранение проблем насыщения трансформатора. В данных преобразователях малый разбаланс напряжения вызывает смещение постоянного тока размагничивания трансформатора, и если ток достаточно велик, это может насыщать трансформатор. Постоянная составляющая тока также может увеличивать или уменьшать ток переключения транзистора, поэтому запрограммированный СУ перенастраивает рабочие циклы транзисторов таким образом, чтобы поддерживался вольт-секундный баланс трансформатора. Понижающие преобразователи, силовые каскады которых выполнены по мостовой и полумостовой схемам, (с программированным управлением, работающих в режиме текущего контроля) должны работать без конденсатора в первичной обмотке трансформатора, так как это может привести нестабильности рабочих режимов преобразователя [3–6].
Недостатком СУ с текущим контролем тока является его восприимчивость шумов в сигналах iC(t), iS(t). Эти шумы могут возникать на входе триггера и переключать последний, что может привести к сбою работы СУ преобразователя. Поэтому требуется небольшая фильтрация токов переключения, чтобы устранить всплески тока, обусловленные зарядом диода.
В современных интегральных схемах широко реализуется программируемое СУ с текущим контролем тока.
Рассмотрим процессы при значении коэффициента управления (рабочий цикл) D > 0,5. Отметим, что режимы СУ текущего программируемого контроля нестабильны, когда установившийся рабочий цикл D больше 0,5. Чтобы избежать этой проблемы, схема управления обычно модифицируется добавлением искусственного наклона (рампа) к измеренному сигналу тока датчика [3, 4].
Здесь рассматривается стабильность управления в режиме текущего контроля при условии линейности тока силового ключа, что позволит при анализе применять более простой метод, а именно использовать простую модель первого порядка, чтобы получить передаточную функцию преобразователя и функцию выходного импеданса без значительного ущерба точности расчета.

Рис. 3. Ток индуктора в непрерывном режиме запрограммированного контроля
На рис. 3 видно, что преобразователь работает в непрерывном режиме тока. В первом межкоммутационном интервале времени наклон характеризуется коэффициентом m1, а во втором межкоммутационном интервале времени — коэффициентом –m2. Для основных неизолированных преобразователей (рис. 4) наклоны, m1 и –m2 задаются следующими формулами.

Рис. 4. Силовые схемы понижающих и повышающих преобразователей:
а) понижающий;
б) повышающе-понижающий
Для понижающих преобразователей (рис. 4а):
Для повышающих преобразователей (рис. 4б):
Имея значения величин m1 и –m2, можно определить соотношения между основными величинами iL(0), iC, iL(T), d, Ts.
В первом межкоммутационном интервале ток индуктора iL(T) возрастает с коэффициентом наклона m1 и достигает контрольного значения iC(t), следовательно:
Из (3) определяется мгновенное значение рабочего цикла d(t):
Аналогично для второго межкоммутационного интервала можно записать:
В установившемся режиме iL(0) = iL(Ts), d(t) = D, d` = 1 – d(t) = D`, m1 = M1, m2 = M2, и с учетом этого из (5) получим:
0 = M1DTS – M2D`TS. (6)
Из (6) следует:
M2/M1 = D/D`. (7)
Условие (7) совпадает с условием равновесия вольт-секундного баланса индуктора в установившемся режиме [7].
Допустим, начальный ток индуктора iL(0) имеет некоторое возмущение :
где IL0 — среднее значение тока iL(0) в установившемся режиме, которое соответствует выражениям (4) и (5) при условии, что:
Желательно оценить стабильность работы СУ в режиме текущего контроля, при помощи проверки необходимо оценить, уменьшается ли это небольшое возмущение в конечном итоге до нуля. Для этого требуется найти возмущения после n периодов переключения ![]() и определить, стремится ли
и определить, стремится ли ![]() к нулю при больших n.
к нулю при больших n.
В установившемся режиме форму тока и колебания возмущения через индуктор можно представить, как это показано на рис. 5.

Рис. 5. Форма тока и колебания возмущения через индуктор при положительном значении
Для наглядности величина (масштаб) тока возмущения индуктора ![]() искусственно увеличена. Предполагается, что преобразователь работает вблизи стационарного состояния, поэтому наклоны m1 и m2 практически не изменяются. На рис. 5 показаны графики при положительном значении
искусственно увеличена. Предполагается, что преобразователь работает вблизи стационарного состояния, поэтому наклоны m1 и m2 практически не изменяются. На рис. 5 показаны графики при положительном значении ![]() . Тогда величина будет отрицательной.
. Тогда величина будет отрицательной.
Поскольку на интервале ![]() наклоны установившегося и возмущенного сигналов, по существу, равны, разница между этими сигналами равна начальному току
наклоны установившегося и возмущенного сигналов, по существу, равны, разница между этими сигналами равна начальному току ![]() для данного интервала. Аналогичным образом разница между двумя колебательными формами является постоянной величиной
для данного интервала. Аналогичным образом разница между двумя колебательными формами является постоянной величиной ![]() на временном интервале
на временном интервале ![]() , поскольку обе колебательные формы имеют одинаковые наклоны –m2 (рис. 5).
, поскольку обе колебательные формы имеют одинаковые наклоны –m2 (рис. 5).
Как видно из рис. 5, ![]() — отрицательная величина, с учетом этого можно определить
— отрицательная величина, с учетом этого можно определить ![]() , используя
, используя ![]() и рассматривая только интервал
и рассматривая только интервал ![]() , коэффициент m1 и ширину интервала
, коэффициент m1 и ширину интервала ![]() :
:
Аналогично можно определить возмущение ![]() :
:
Устраняя неопределенный параметр ![]() из (10) и (11), получим:
из (10) и (11), получим:
С учетом (7) из (12) получим:
Сделав аналогичный анализ для следующего межкоммутационного интервала, получим:
Аналогично после коммутационного интервала получим:
Отметим, когда n стремится к бесконечности, а возмущение ![]() стремится к нулю при условии, как это следует из (14), что отношение (D/D`) меньше единицы. Аналогично, если возмущение
стремится к нулю при условии, как это следует из (14), что отношение (D/D`) меньше единицы. Аналогично, если возмущение ![]() стремится к бесконечности, то отношение (D/D`) больше единицы:
стремится к бесконечности, то отношение (D/D`) больше единицы:
Следовательно, для стабильной работы в режиме текущего контроля необходимо обеспечить условие |–D/D`| или |D |< 0,5, обычно отношение (–D/D`) называют фактором нестабильности и обозначают α:
α = –D/D`.
В качестве примера рассмотрим повышающий конвертер при следующих параметрах: входное постоянное напряжение Vg = 20 В, выходное напряжение V = 50 В.
При этих параметрах V/Vg = 1/D` или D` = 0,4, D = 1 – D` = 0,6. При этих параметрах ожидается, что СУ с непрерывным контролем будет нестабильным, как можно видеть на графиках рис. 6.

Рис. 6. Осциллограммы при D = 1 – D`= 0,6
Следовательно, коэффициент фактора нестабильности определяется:
Согласно уравнению (14), после одного периода переключения ток возмущения индуктивности должен возрастать в соответствии с фактором нестабильности α в –1,5 раза (рис. 6), то есть на величину ![]() , после второго периода переключения ток возмущения возрастает в
, после второго периода переключения ток возмущения возрастает в ![]() раза, а после третьего периода возрастает на величину
раза, а после третьего периода возрастает на величину ![]() .
.
Для конкретных начальных условий, показанных на рис. 6, это возрастающее колебание после трех периодов переключения насыщает текущий запрограммированный контроллер (СУ). Силовой транзистор остается включенным в течение всего четвертого периода переключения. Причем при длительности, равной целому числу периодов переключения, ток индуктора и сигналы СУ по своему характеру могут в конечном итоге стать колебательными и периодическими. Соответственно, формы колебания сигналов могут стать хаотичными. В каждом из этих случаев СУ не работает как предназначено.
На рис. 7 показаны осциллограммы тока через индуктивность в повышающем конвертере при уменьшении выходного напряжения до V = 30 В и D = 1–D`=1/3 (Vg = 20 В). При этом коэффициент нестабильности определяется:

Рис. 7. Осциллограммы повышающего конвертера при D = 1 – D`=1/3
В этом случае возмущение по величине уменьшается в каждом периоде переключения по фактору нестабильности, равной 0,5. А ток индуктора по амплитуде уменьшается через несколько периодов переключения и в конце четвертого такта практически становится незначительным.
Нестабильность преобразователя при D > 0,5 можно устранять соответствующим выбором структуры СУ — с помощью ввода дополнительного искусственного наклона в измеряемом токе индуктора, как это показано на рис. 8.

Рис. 8. Упрощенная схема конвертера с системой управления непрерывного контроля с вводом искусственного наклона в измеряемом токе индуктора:
а) блок-схема СУ,
б) диаграммы тока искусственного наклона (рампа)
Искусственно добавленное линейное изменение тока имеет качественный эффект для уменьшения усиления внутренней дискретной петли обратной связи, чувствительной к току переключения. Коэффициент искусственного наклона равен ma, при этом СУ переключает силовой ключ при выполнении следующих условий:
где ia(t) — искусственная форма волны линейного изменения. Следовательно, транзистор переключается, когда ток индуктивности задается как:
На рис. 9 приведено аналоговое сравнение формы волны тока индуктора с величиной разности токов [ic – ia (dTS)].
![Аналоговое сравнение формы волны тока индуктора с величиной разности токов [ic – ia (dTS)]](https://power-e.ru/wp-content/uploads/11_81_9-600x306.jpg)
Рис. 9. Аналоговое сравнение формы волны тока индуктора с величиной разности токов [ic – ia (dTS)]
Здесь также возможно определить стабильность тока, анализируя изменение возмущения формы волны тока индуктора в течение полного периода переключения [7].
На рис. 10 показаны колебания тока в установившемся и возмущенном режимах в дросселе при наличии искусственного линейного изменения с коэффициентом ma.

Рис. 10. Колебания тока дросселя в установившемся и возмущенном режимах при наличии искусственного линейного изменения с коэффициентом ma
Как показано на рис. 10, при положительном начальном значении возмущенного ![]() тока значения
тока значения ![]() и
и ![]() , как правило, становятся отрицательными.
, как правило, становятся отрицательными.
Если возмущенные формы волны достаточно близки к рабочей точке покоя, то наклоны m1 и m2 практически не изменяются и взаимосвязь между ![]() и
и ![]() может быть определена исключительно с учетом интервала
может быть определена исключительно с учетом интервала ![]() . Возмущения
. Возмущения ![]() и
и ![]() выражаются через наклоны m1, m2, ma и длину интервала (
выражаются через наклоны m1, m2, ma и длину интервала (![]() ) следующим образом:
) следующим образом:
Из (18) и (19) получим:
Аналогичный анализ может быть применен к n-му периоду переключения, в результате получим:
Здесь коэффициент фактора нестабильности определяется:
При больших значениях числа n величина возмущения стремится:
Следовательно, для стабильности управления в режиме текущего контроля нужно выбрать величину коэффициента искусственно созданного наклона линейного изменения ma таким образом, чтобы характеристический коэффициент фактора стабильности α был меньше единицы.
В обычном применении регулятора напряжения выходное напряжение v(t) хорошо регулируется, при этом входное напряжение vg(t) неизвестно. Из уравнения (1) видно, что коэффициент наклона m2 является постоянной величиной и с высокой степенью точности определен для понижающе-повышающих конвертеров. Поэтому, используя уравнения (6) и (25), устраним коэффициент наклона m1 и найдем зависимость характеристического коэффициента α от известного коэффициента наклона m2 и от установившегося рабочего цикла D:
Один из наиболее распространенных способов выбора величины коэффициента наклона искусственного линейного изменения выглядит следующим образом:
Подстановкой (25) в уравнение (24) можно проверить, что этот выбор приводит к α = 1 при D =1 (D` = 0) и к |α|<1 для 0 ≤ D< 1. Это наименьшее значение, которое обеспечивает устойчивый (стабильный) режим работы конвертера во всем рабочем цикле.
Другим распространенным вариантом выбора ma является:
ma = m2 (26)
В этом случае значение коэффициента фактора нестабильности α становится равным нулю при всех значениях коэффициента D. В результате ![]() равен нулю для любого значения
равен нулю для любого значения ![]() , который не насыщает преобразователь. Эта система устраняет любую ошибку после одного периода переключения. Такое поведение системы известно как «мертвый контроль», или контроль с конечным временем установки [3, 8].
, который не насыщает преобразователь. Эта система устраняет любую ошибку после одного периода переключения. Такое поведение системы известно как «мертвый контроль», или контроль с конечным временем установки [3, 8].
Следует отметить, что в приведенном выше анализе устойчивости использовалось квазистатическое приближение, в котором наклоны m1 и m2 колебания тока индуктора в стационарном режиме предполагаются идентичными. В большинстве общих случаев стабильность и переходные характеристики всей системы, работающие в режиме управления текущего контроля, должны оцениваться с помощью общесистемного анализа в широком диапазоне дискретного времени [8, 9].
Отметим также, что рассмотренные системы чувствительны к шумам. Когда шум присутствует в схеме СУ, может наблюдаться значительное изменение в форме сигнала рабочего цикла. Устранить этот эффект удается за счет уменьшения усиления внутренней дискретной петли обратной связи путем введения дополнительного искусственного линейного изменения, амплитуда которого превышает пульсации тока индуктора.
Тем не менее на практике вышеупомянутые аргументы оказываются достаточными для выбора искусственного наклона ma [5, 6].
Рассмотрим простую модель первого порядка на примере повышающего конвертера. Силовая схема простого повышающего преобразователя, работающего в режиме непрерывной проводимости, показана на рис. 4б, а ток через индуктивность — на рис. 3. Малосигнальное усредненное уравнение для этого конвертера приведено в работе [7] и имеет следующий вид:
Преобразование Лапласа при нулевых начальных условиях уравнения (27) имеет следующий вид:
Допустим, что ток индуктивности ![]() идентичен задающему току контроля
идентичен задающему току контроля ![]() . Это допущение действительно настолько, насколько стабильно работает СУ и пульсации тока индуктивности и искусственное линейное изменение незначительны:
. Это допущение действительно настолько, насколько стабильно работает СУ и пульсации тока индуктивности и искусственное линейное изменение незначительны:
С учетом выражений (29) из (28) получим функциональную зависимость между током ![]() и коэффициентом рабочего цикла
и коэффициентом рабочего цикла ![]() :
:
Решая (30) относительно ![]() , получим:
, получим:
В зависимости от изменения входного контрольного сигнала ![]() это выражение для малого сигнала описывает, каким образом с помощью запрограммированного контроллера (СУ) необходимо менять рабочий цикл малого сигнала
это выражение для малого сигнала описывает, каким образом с помощью запрограммированного контроллера (СУ) необходимо менять рабочий цикл малого сигнала ![]() . Как видно из (31),
. Как видно из (31), ![]() зависит не только от коэффициента рабочего цикла D, но и от входного и выходного напряжений контроллера. Замещая
зависит не только от коэффициента рабочего цикла D, но и от входного и выходного напряжений контроллера. Замещая ![]() во втором и третьем уравнениях и используя выражение (31), можно получить:
во втором и третьем уравнениях и используя выражение (31), можно получить:
Выражения (32а, б) можно упростить, используя соотношения установившихся режимов:
Используя (32) и (33), получим:
Уравнение (34) — это малосигнальное базисное уравнение для синтеза линейной модели первой степени понижающе-повышающего преобразователя с текущим контролем.
Эти уравнения можно использовать для построения малосигнальных моделей схем переменного тока, которые представляют поведение входных и выходных портов преобразователя.
На рис. 11б ток ![]() показан в виде независимого источника тока,
показан в виде независимого источника тока, ![]() — ток нагрузки,
— ток нагрузки, ![]() — ток, проходящий через действующий эффективный резистор переменного тока со значением R/D. Величина –(D2/D`R)
— ток, проходящий через действующий эффективный резистор переменного тока со значением R/D. Величина –(D2/D`R) ![]() моделируется с помощью эффективного резистора переменного тока с негативным значением –(D`R/D2).
моделируется с помощью эффективного резистора переменного тока с негативным значением –(D`R/D2).

Рис. 11. Малосигнальная эквивалентная схема повышающе-понижающего преобразователя с текущим контролем:
а) модель входного порта согласно второму уравнению (34);
б) модель выходного порта в соответствии с первым уравнением (34)
Схему на рис. 11 можно заменить малосигнальной моделью с двумя портами, как это показано на рис. 12.

Рис. 12. Малосигнальная схемная модель с двумя портами
Передаточная функция, которая описывает связь контрольного сигнала управления с выходным напряжением, то есть связь между током ![]() и
и ![]() , определяется установкой
, определяется установкой ![]() . С учетом этого решение для выходного напряжения приводит к определению передаточной функции Gvc(s):
. С учетом этого решение для выходного напряжения приводит к определению передаточной функции Gvc(s):
В таблице, согласно схемам на рис. 11 и 12, приведены параметры f2 и r2; подставляя эти параметры для повышающе-понижающего преобразователя (рис. 4б) в (35), получим:
|
Тип конвертера |
g1 |
f1 |
r1 |
g2 |
f2 |
r2 |
|
Понижающий |
D/R |
|
–R/D2 |
0 |
1 |
∞ |
|
Повышающий |
0 |
1 |
∞ |
1/RD` |
|
R |
|
Понижающе-повышающий |
-D/R |
|
–RD`/D2 |
–D2/RD` |
|
R/D |
Как видно из (36), передаточная функция содержит один полюс и один ноль, причем ноль находится в правой части фазовой плоскости, и ее угловая частота остается неизменной во время контролируемого рабочего цикла. Усиление по постоянному току зависит только от сопротивления нагрузки R.
Передаточная функция от входа к выходу Gvg(s) определяется из схемной модели на рис. 11, приравнивая управляющий входной ток к нулю ![]() :
:
Подставляя из таблицы параметры g2 и r2 в (35) для модели повышающе-понижающего преобразователя, получим:
Для выходного импеданса из схемы на рис. 12 получим:
В соответствии с формулами (36), (38) и (40) получены диаграммы Боде для повышающе-понижающего конвертера, которые приведены на рис. 13. С помощью этих зависимостей можно соответственно выбирать параметры элементов и рабочую частоту преобразователя, при которой обеспечиваются нужные величины передаточных функций.
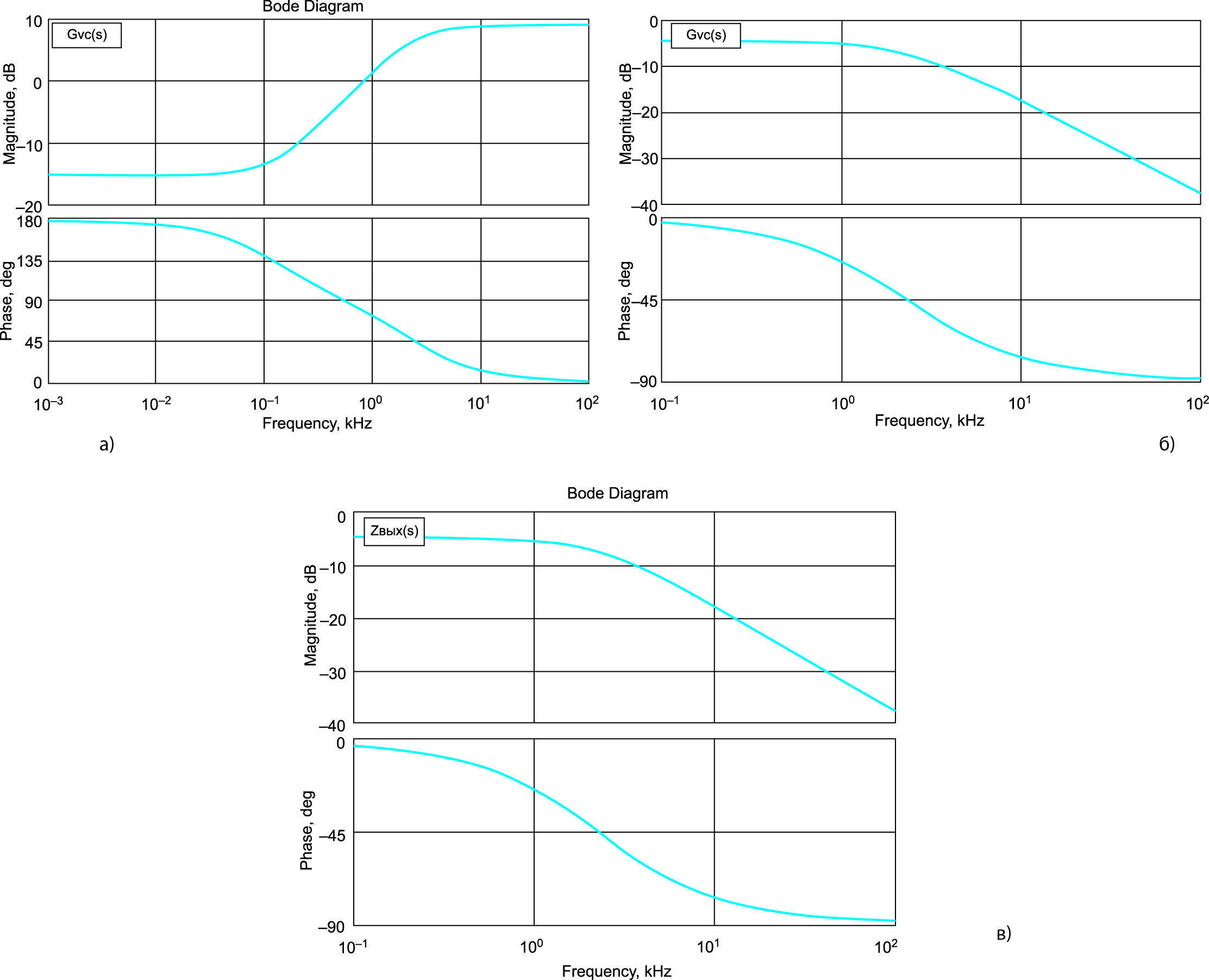
Рис. 13. Диаграммы Боде:
а) зависимости в соответствии с (36);
б) зависимости в соответствии с (38);
в) зависимости в соответствии с (40)
Выводы
- При управлении в режиме текущего контроля пиковое значение тока переключения iS(t) следует за управляющим входным током контроля iC(t). Этот широко используемый метод управления имеет преимущество из-за простоты управления.
- Управление с текущим контролем нестабильно при D > 0,5 независимо от структуры преобразователя. Преобразователь может быть стабилизирован добавлением искусственной рампы с наклоном ma в токе iC(t). Когда ma > 0,5m2, преобразователь работает стабильно во всех рабочих циклах.
- Простая модель первого порядка конвертера показывает, что один ноль исключается из нулей передаточных функций преобразователя: передаточной функции от входной цепи к выходу и передаточной функции от цепи управления к выходу (передаточная функция, описывающая связь контрольного сигнала управления с выходным напряжением).
- Hsu S., Brown A., Rensink L., Middlebrook R. D. Modeling and Analysis of Switching Dc-to-Dc Converters in Constant-Frequency Current Programmed Mode. IEEE Power Electronics Specialists Conference Record, 1979.
- Ericson R. W., Maksimovic D. Fundamentals of Power Electronics. Springer Science & Business Media, 2007.
- Middlebrook R. D. Topics in Multiple-Loop Regulators and Current-Mode Programming. IEEE Power Electronics Specialists Conference Record, 1985.
- Middlebrook R. D. Modeling Curreent Programmed Buck and Boost Regulatorts // IEEE Power Electronics Specialists Conference. Vol. 4. No. 1.
- Vergnese G., Bruzos C., Mahabir K. Averaged and Sampled-Data Models for Current Mode Control: A Reexamination. Power Electronics Specialists Conference Record, 1989.
- Brown A., Middlebrook R. D. Sampled-Data Modeling of Switching Regulators. IEEE Power Electronics Specialists Conference Record, 1981.
- Петросян Н. Н., Бегоян К. В., Кароян Г. С. Анализ повышающе-понижающих конвертеров с помощью эквивалентной трансформаторной схемы малого сигнала // Силовая электроника. 2019. №1.
- Vorperian V. Simplified Analysis of PWM Converters Using Model of PWM Switch: Part I and II // IEEE Transactions on Aerospace and Electronic Systems. 1990. Vol. 26. No. 3.
- Sun J., Mitchell D. M., Greuel M. F., Krein P. T., Bass R. M. Averaged Modeling of PWM Converters Operating in Discontinuous Conduction Mode // IEEE Transactions on Power Electronics. 2001. Vol. 16. No. 4.










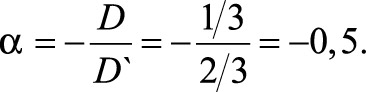


















 7 января, 2022
7 января, 2022 20 июня, 2022
20 июня, 2022