К вопросу о конструировании кабельных муфт высокого напряжения

Рис. 1. Концевая муфта и стресс-конус
Причиной отклонения распределения электрического поля от равномерного является разность емкостных токов через усиливающую изоляцию муфты на землю и через изоляцию кабеля на жилу [1, 2]. Поскольку изменять величину емкости на жилу не представляется возможным, то вариантами изменения характера распределения поля по длине разделки являются:
- Изменение продольной комплексной проводимости кабельной разделки, как реактивной (конденсаторные элементы) составляющей, так и омической — продольной активной проводимости, в чем и состоит сущность импедансного метода. Известная [1] схема замещения кабельной разделки представляет собой цепочку из продольных и поперечных параллельных RС-элементов по два поперечных элемента в каждой ячейке. Один из элементов моделирует комплексное сопротивление току смещения через изоляцию кабеля на жилу, а второй — комплексное сопротивление току смещения через усиливающую изоляцию кабельной муфты на землю. Выравнивание поля изменением активной составляющей продольной проводимости реализуется путем нанесения, тем или иным способом, на изоляцию кабеля специальных проводящих покрытий (слоев) — полимерных экранов. Регулирование поля путем изменения реактивной (емкостной) составляющей продольной проводимости в данной работе не рассматривается, так как подобный подход применяется только в технологиях кабелей с бумажно-пропитанной и масляно-бумажной изоляцией с применением соответствующих материалов для усиливающей изоляции кабельных муфт (так называемая подмотка конденсаторного типа).
- Геометрический и рефракционный способы связаны с изменением конфигурации поля за счет увеличения емкости C0 усиливающей изоляции на землю. Нейтрализующее действие этой емкости используется при применении проводящих экранов, в том числе рефлектора стресс-конуса. Кривизна рефлектора должна обеспечивать компенсацию емкостного тока на жилу током смещения через усиливающую изоляцию на землю. В этом суть геометрического способа. Рефракционный способ предполагает увеличение емкости C0 за счет применения в качестве материала основного изоляционного тела стресс-конуса силиконовой резины со специальным наполнителем, обеспечивающим значение величины диэлектрической проницаемости, на порядок превышающее соответствующий параметр XLPE-изоляции кабеля. Однако эффект от выравнивания продольной составляющей электрического поля рефракционным методом весьма зависим от гармонического состава кривой питающего напряжения.
Сочетание геометрического и рефракционного методов [2, 3] позволяет уменьшить тангенциальную составляющую напряженности электрического поля в местах обрыва оболочек и экранов (нарушения заводской изоляции кабельных изделий), не прибегая к сложным технологическим процедурам формирования особых свойств материалов. Например, основной модуль — стресс-конус концевой муфты — может представлять собой конусообразное двухслойное тело (рис. 1). Его внешняя часть, занимающая основной объем, изготавливается из резины с изоляционными свойствами (основное изоляционное тело конуса), а внутренняя часть — рефлектор — формуется из резины с простыми проводящими наполнителями (мелкодисперсная сажа, металлический порошок) и выполняет функцию выравнивания электрического поля в усиливающей изоляции. В случае концевой муфты наружной установки пространство между стресс-конусом и внешним изолятором муфты заполнено жидким диэлектриком, оптимальная диэлектрическая проницаемость которого также является предметом анализа.

Рис. 2. Геометрическая расчетная модель стресс-конуса
Опыт конструирования и эксплуатации высоковольтных кабельных муфт показывает, что проблемными с точки зрения концентрации электрического поля могут быть следующие зоны (рис. 2):
- место обрыва полимерного экрана по изоляции кабеля (зона A);
- зона окончания рефлектора стресс-конуса (зона Б);
- заполненное жидким диэлектриком пространство между стресс-конусом и наружным изолятором (зона В);
- зона окончания конуса вблизи основной изоляции кабеля (зона Г).
Зависимость максимального поля в проблемных зонах Б, В и Г от диэлектрической проницаемости жидкого диэлектрика показана на рис. 3.

Рис. 3. Максимальная напряженность поля в зонах Б, В и Г
Как показывает график, напряженность поля в проблемных зонах Г и Б выше соответствующих значений для зоны В. При этом максимальная напряженность (имеет место в зоне Г) сопоставима либо больше, чем соответствующий параметр для зоны А, только в тех случаях, когда относительная диэлектрическая проницаемость жидкого диэлектрика меньше 3.
Анализ причин отказов позволяет сделать вывод [2], что в большинстве случаев выход из строя муфты происходит из-за дефектов в критической зоне А — на границе раздела «изоляция кабеля — полупроводящий полимерный экран по изоляции кабеля». Поэтому в качестве критерия оптимальности выбран минимум модуля напряженности электрического поля Еиз_пп в указанной зоне. При численном моделировании [2, 4] методом конечных элементов электрического поля в муфте была решена серия задач с целью оптимизации геометрии и проводящих свойств [3]. На рис. 4 показано распределение поля вдоль горизонтального отрезка ОX поверхности полимерного экрана по изоляции. Стресс-конус муфты выполнен из силиконовой резины и состоит из проводящего рефлектора и основного изоляционного тела. На рис. 4 варианты — согласно таблице.

Рис. 4. Распределение поля в разных вариантах свойств конуса и рефлектора
| Варианты | Тело конуса | Рефлектор | ||
| Относительная диэлектрическая проницаемость ε | Электропроводность σ, См/м | Относительная диэлектрическая проницаемость ε | Электропроводность σ, См/м | |
| 1 | 1 | 0 | 1 | 0 |
| 2 | 2,5 | 2,5 | ||
| 3 | 22 | |||
| 4 | 22 | 0,0002 | ||
Расчеты производились по следующему алгоритму:
- При фиксированном значении диэлектрической проницаемости основного изоляционного тела стресс-конуса изменялись значения омической проводимости рефлектора. Целью расчета была фиксация оптимального значения проводимости, при котором модуль Еиз пп минимален.
- При выбранном в п. 1 соотношении между компонентами активной проводимости варьировалась длина рефлектора (длина проекции рефлектора на ось). Целью расчета была фиксация длины рефлектора, при которой модуль напряженности поля Еиз пп достигает минимума.
- При фиксированных значениях соотношения компонентов проводимости и длины рефлектора по п.п. 1 и 2 изменялся угол наклона касательной к начальному участку рефлектора (считая от кабеля) по отношению к оси кабеля. Целью расчета была фиксация величины угла, при которой модуль напряженности поля Еи_пп достигает минимума.
- При фиксированных значениях по п.п. 1, 2 и 3 варьировалась величина относительной диэлектрической проницаемости ε основного изоляционного тела стресс-конуса. Целью расчета была фиксация величины ε, соответствующей минимуму напряженности поля Еиз_пп.
Потенциал жилы задавался равным амплитудному значению фазного напряжения, потенциал экрана принимался равным нулю. Рефлектор стресс-конуса по его назначению должен быть электрически соединен с заземленным экраном кабеля, выполняя функцию восстановления «обрезанного» экрана кабеля (имитация первоначальной конструкции до разделки). По предложенному алгоритму решалась задача расчета электрического поля переменного тока.
На рис. 5 приведена зависимость максимальной напряженности электрического поля в зависимости от диэлектрической проницаемости основного изоляционного тела конуса в широком диапазоне: 1< εтела<24.

Рис. 5. Зависимость максимальной напряженности поля от диэлектрической проницаемости основного тела
На этом графике синяя и оранжевая кривые соответствуют рефлектору с нулевой проводимостью, а зеленая кривая — полупроводящему рефлектору с удельной электропроводностью γ = 0,0002 См/м. Из графика следует, что снижения напряженности поля до требуемого уровня практически невозможно добиться без использования полупроводящего рефлектора.
Отметим также, что выбор конструкции стресс-конуса и свойств диэлектрических материалов оказывает влияние на электрическую емкость муфты. Емкость между жилой и землей легко может быть оценена через полную энергию электрического поля в расчетной области WЭ, и известное фазное напряжение Uф:
Зависимость емкости от диэлектрической проницаемости основного изоляционного тела стресс-конуса приведена на рис. 6.

Рис. 6. Емкость муфты в зависимости от диэлектрической проницаемости основного тела конуса
Графики на рис. 6 показывают, что емкость конструкции муфты и, соответственно, запасенная в ней энергия электрического поля, осциллирующая с двойной частотой, увеличивается почти на треть по мере приближения степени ослабления максимального электрического поля к оптимальному значению. Этот факт может быть учтен при моделировании режимов работы муфты в составе электрической цепи. Численные расчеты проводились с использованием специализированного вычислительного комплекса на базе модуля ELCUT версии 5.9 [5].
Выводы
В работе описан способ снижения неравномерности электрического поля в месте обрыва экранов и проводящих оболочек, основанный на сочетании свойств материалов стресс-конуса кабельной муфты и специального подбора геометрической конфигурации элементов стресс-конуса.
Установлено, что для муфт класса напряжений 64/110 кВ:
- Оптимальное отношение продольной (σх) к поперечной (σy) составляющей активной проводимости рефлектора находится в пределах σх/σy = 10…12. Результаты расчета в оптимальном случае дают значение Emin = 2,85 кВ/мм.
- Оптимальное значение длины проекции рефлектора на ось кабеля находится в пределах L = 85…120 мм.
- Оптимальное значение угла наклона касательной к начальному участку рефлектора стресс-конуса — φ = 8…14°.
- Оптимальное значение относительной диэлектрической проницаемости ε материала основного изоляционного тела принимает значения из промежутка ε = 22…24.
Для более точной оценки оптимальных значений σx/σy, L, φ и ε следует выполнить оптимизационные расчеты электромагнитного поля в соответствии с приведенным в настоящей работе алгоритмом. В общем случае для изготовления рефлектора может быть использована смесь эластичного полимерного материала с мелкодисперсным токопроводящим наполнителем. В качестве эластичного полимерного материала применимы этиленпропиленовая или силиконовая резины, а в качестве мелкодисперсного токопроводящего наполнителя — сажа или металлический порошок.
- Шварцман Л. Г. Регулирование электрического поля в концевых муфтах кабелей высокого напряжения. М.: Энергия. Труды ВНИИКП. 1969. Вып. 13.
- Грешняков Г. В., Дубицкий С. Д. Комбинированный способ снижения неравномерности электрического поля в муфтах силовых кабелей. // Силовая электроника. 2010. № 2.
- Пат. на полезную модель № 97013 (РФ) Соединительная муфта для силового кабеля / Г. В. Грешняков, И. В. Журавлев, А. В. Матвеев // Рег. 20.08.2010.
- Грешняков Г. В., Дубицкий С. Д. Математическое моделирование электрического поля в муфтах силовых кабелей // Силовая электроника. 2010. № 3.
- Дубицкий С. Д. Elcut 5.1 — платформа разработки приложений анализа полей // Exponenta Pro. 2004. № 1.

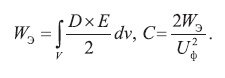
 7 октября, 2012
7 октября, 2012 6 сентября, 2011
6 сентября, 2011 5 августа, 2009
5 августа, 2009