Полупроводниковые резонансные преобразователи для солнечных электростанций
1По прогнозам Международного энергетического агентства (IEA) энергия солнечного излучения к 2050 г. обеспечит до 25 % потребности человечества в электричестве и сократит выбросы углекислого газа [3]. Промышленно развитые страны непрерывно наращивают внедрение солнечных электростанций, а также производство полупроводниковых преобразователей для них. Следовательно, непрерывно повышаются масштабы и уровень научно-исследовательских и опытно-конструкторских работ по проблемам солнечных электростанций.
Солнечные батареи могут вырабатывать лишь постоянный ток, но для питания таких привычных нам приборов, как компьютер, телевизор, чайник и т. п., необходимо переменное сетевое напряжение 220 В или трехфазное 380 В. Для преобразования постоянного напряжения в переменное синусоидальной формы нужны преобразователи. В настоящее время по материалам фирм, выпускающих полупроводниковые преобразователи, стоимость серийных преобразователей для солнечных электростанций составляет примерно 150–300 долл. на 1 кВт.
До 2017 г. ООО «Хевел» (г. Новочебоксарск) выпускало микроморфные фотоэлектрические солнечные модули, изготовленные по тонкопленочной технологии. Их КПД составлял 9,5 %, а номинальная мощность — 120 Вт. Во втором квартале 2017 г. действующая производственная линия завода в г. Новочебоксарске была переоборудована под производство гетероструктурных солнечных модулей (по принципиально новой технологии), собираемых из ячеек. Годовой объем выпуска продукции — 160 МВт. Номинальная мощность солнечного модуля составляет 300 Вт. От большинства аналогов его отличает более высокая эффективность в выработке электроэнергии — средний КПД ячеек превышает 22%. Кроме того, новые модули эффективнее работают при высоких и низких температурах, что существенно расширяет географию их применения.
Гетероструктурная ячейка может быть поставлена в любую страну для сборки модулей. Длина ячейки (156,75 ± 0,25) мм, ширина (156,75 ± 0,25) мм, толщина (0,18 ± 0,02) мм, диагональ (210 ± 0,5) мм, масса (10,2 ± 0,2) г, КПД 22,6–22,8 %, мощность 5,51–5,56 Вт.
Зарубежные производители полупроводниковых преобразователей для солнечных электростанций, как правило, не раскрывают принципиальные схемы этих преобразователей. Особенно затрудняет использование зарубежных аналогов при разработках и проектировании преобразователей для солнечных электростанций то, что неизвестны алгоритмы управления и программы для микропроцессоров, входящих в состав систем управления преобразователями. Приходится самим разрабатывать теоретические основы, методики расчетов отдельных узлов, характеристик и переходных процессов, анализа и синтеза замкнутых систем управления преобразователями. Вместе с тем в зарубежных публикациях дано описание многих схем силовой частей подобных преобразователей.
Основные структуры фотопреобразовательных (ФП) инверторов представлены на рис. 1 [4].

Рис. 1. Обзор структур ФП-инверторов:
централизованная (а);
раздельная (б);
многоцепочечная (в);
с отдельными инверторами для каждого модуля (г)
Ранее использовалась структура (рис. 1а), основанная на централизованных регулируемых инверторах, которые связывают большое число ФП-модулей с сетью переменного тока. ФП-модули разделены на цепочки последовательно соединенных модулей, каждая из которых генерирует достаточно высокое напряжение, чтобы избежать дальнейшего его повышения. Затем эти цепочки для повышения мощности соединяют параллельно через разделительные диоды. Основные недостатки такой структуры: потери мощности из-за рассогласования между модулями; негибкость, которая не позволяет реализовать выгоды массового производства преобразователей; наличие кабелей высокого напряжения между ФП-модулями и инвертором; потери мощности из-за централизованного слежения за точкой максимальной мощности (СТММ); потери в разделительных диодах. Тиристорный инвертор создает большое число токовых гармоник, обуславливающих плохое качество энергии.
Современная структура (рис. 1б) включает в себя регулируемые инверторы для каждой цепочки ФП-модулей. Здесь отсутствуют потери мощности в разделительных диодах и потери из-за рассогласования цепочек, поскольку точка максимальной мощности (ТММ) определяется для каждой из них отдельно. Это повышает общий КПД по сравнению с КПД системы, использующей централизованный инвертор, и снижает стоимость в связи с массовым производством.
В случае использования отдельного регулируемого инвертора для каждого ФП-модуля (рис. 1г) устраняются потери мощности вследствие рассогласования между ФП-модулями, так как отслеживается ТММ каждого ФП-модуля. Кроме того, облегчается возможность наращивания мощности системы благодаря модульной структуре. Появляется возможность создания устройства plug and play («подключай и играй», подключай вилку в розетку и работай), которое в будущем может быть использовано людьми, не имеющими каких-либо знаний об электрических установках. Однако необходимость повышения напряжения модуля может уменьшить общий КПД и увеличить цену за 1 Вт мощности из-за более сложной схемы. Структура требует массового производства, при котором снижаются затраты на изготовление и розничные цены.
В связи с изложенным, в выполненной работе были исследованы и разрабатывались схемы преобразователей, работающих от одного ФП-модуля. (В зарубежных публикациях рассматриваемые преобразователи называются микроинверторами.)
Преобразователи, работающие от одного ФП-модуля, можно разделить на две основные группы:
- На базе инвертора с синусоидальной ШИМ (СШИМ).
- Высокочастотные с последовательным резонансным инвертором.
В статье рассматриваются преобразователи постоянного напряжения (ППН) с последовательным резонансным инвертором, или так называемые резонансные преобразователи. Они имеют высокий КПД на сравнительно высоких частотах переключений f. Регулирование выходного напряжения таких ППН выполняется тремя методами: фазовым, частотным и комбинированным. Имеется большое количество зарубежных и отечественных публикаций, посвященных таким ППН, однако уровень теоретических исследований пока недостаточен, в связи с чем отсутствуют в достаточной мере обоснованные методики их расчета и проектирования.

Рис. 2. Схема силовой части ППН
(а) и временные диаграммы
(б) для ППН с последовательным резонансным инвертором в РНТ
Исследованная схема резонансного ППН с фазовым регулированием [5] представлена на рис. 2а, а временные диаграммы при работе в режиме непрерывного тока — на рис. 2б. Приведенная схема (рис. 2а) работает на частоте переключений f, превышающей резонансную частоту LC-контура fр. Процессы в этих схемах исследуются методом припасовывания с использованием векторно-матричного дифференциального уравнения LC-контура для i-го рабочего интервала (i = 1, 2, 3)
где x — вектор состояния, A и B — матрицы, определяемые выражениями
νi — внешнее воздействие на i-м рабочем интервале, ν1 = uвх – u’вых, ν2 = –u’вых, ν3 = –(uвх – u’вых).
На каждом полупериоде переключений в режиме, показанном на рис. 2б, последовательно наблюдаются три различных рабочих интервала. На первом интервале (i = 1) открыты транзисторы VT1 и VT4, на втором (i = 2) — транзисторы VT1 и VT3, на третьем (i = 3) — транзисторы VT2 и VT3.
Решение уравнения (1) имеет вид
где ti — момент начала i-го интервала; x(ti) — начальное значение вектора состояния для i-го интервала; xti (∞) — асимптотическое значение вектора состояния для i-го интервала.
Были определены явные выражения для элементов фундаментальной (переходной) матрицы eAt [5].
Из уравнения x(T/2) = x(0) были получены соотношения для расчета мгновенных значений напряжения на конденсаторе LC-контура и тока контура в установившемся режиме. Интегрированием тока в LC-контуре за полпериода T/2 были получены выражения для средних значений выходного и входного токов ППН, впервые построены статические регулировочные (рис. 3) и внешние (рис. 4) характеристики, временные диаграммы (рис. 5) [5], где относительные значения переменных определяются как

Рис. 3. Регулировочные характеристики ППН в РПТ и РНТ (отмечены и пронумерованы точки, для которых построены временные диаграммы на рис. 5)

Рис. 5. Временные диаграммы процессов за полпериода переключений при различных значениях γ для указанных на рис. 3 точек 1 (а); 2, 3 (б); 4–6 (в); 7–9 (г)
Далее исследована схема (рис. 6а), работающая в режиме прерывистого тока в LC-контуре.
При прерывистом токе в LC-контуре схемы на рис. 6 возможны три режима работы: 1) режим с однополярными импульсами тока в LC-контуре на половине периода переключений, который обычно реализуется в схеме без обратных диодов; 2) режим с двуполярными импульсами тока, который реализуется в схеме с обратными диодами при симметричном управлении транзисторами мостовой схемы резонансного инвертора; 3) режим с двухполярными импульсами тока, реализуемый при несимметричном управлении транзисторами и иллюстрируемый на рис. 6б [6].

Рис. 6. Схема силовой части резонансного ППН с преобразователем частоты
на выходе (а);
временные диаграммы, иллюстрирующие установившийся режим прерывистого тока (б);
uc — напряжение сети переменного тока
На рис. 6а представлена схема резонансного преобразователя, работающая на сеть переменного тока. В полупериод положительного напряжения сети транзистор VT5 поддерживается в открытом состоянии, а при открытых транзисторах VT1 и VT4 ток контура трансформируется в обмотку w2 трансформатора и замыкается через диод VD1, транзистор VT5 и выходную цепь ППН. Измененив свое направление, ток трансформируется в обмотку w3 и замыкается через диод VD3, транзистор VT5 и выходную цепь ППН в прежнем направлении.
В полупериод отрицательного напряжения сети транзистор VT6 поддерживается открытым и схема работает аналогично.
Были выведены следующие формулы [6, 7]:
где fп = 1/Tп — частота переключений; nтр = w2/w1 — коэффициент трансформации трансформатора (w1, w2 — число витков первичной и вторичной обмоток); введенный параметр , зависящий от добротности LC-контура, вычисляется по формуле
где Q — добротность резонансного контура, определяемая по формуле Q = (1/r)√LK/СK (Cк — емкость конденсатора контура; L = LK + LS1 + L’S2 и r + rK + r1+ r’2 — суммарная индуктивность и активное сопротивление последовательного резонансного контура, Lк и rк — индуктивность и активное сопротивление дросселя резонансного контура; LS1 и L’S2 — индуктивность рассеяния первичной обмотки и приведенная к первичной обмотке индуктивность рассеяния вторичной обмотки; r1 и r’2 — активное сопротивление первичной обмотки и приведенное к первичной обмотке активное сопротивление вторичной обмотки).
Для построения характеристик в режиме с однополярными импульсами тока следует воспользоваться известными из работы [8] соотношениями:
где верхний индекс «о» обозначает режим с однополярными импульсами.
Характеристики, построенные по формулам (2)–(8), представлены на рис. 7–10.

Рис. 7. Зависимости для определения средних значений выходного и входного токов в установившемся режиме при Qк = 5 (а) и КПД в установившемся режиме от среднего значения выходного напряжения (б), h°K — КПД в режиме с однополярными импульсами тока

Рис. 10. Зависимости КПД от относительного действующего значения напряжения сети (а) и средней за период сети выходной мощности (б) при работе ППН на сеть переменного тока
Результаты, полученные на Simulink-модели преобразователя
Модель ППН с последовательным резонансным инвертором и системой управления, реализующей алгоритм несимметричного управления силовыми транзисторами, собрана в среде Matlab-Simulink (рис. 11). На рис. 11а указаны параметры всех элементов силовой части.

Рис. 11. Модель силовой части (а) и системы управления (б) преобразователя с несимметричным управлением транзисторами, собранная в среде Simulink
Сигналы управления транзисторами Uз1–Uз4, подаваемые на их затворы, формируются системой управления, которая анализирует переход через нуль тока резонансного контура с помощью одного датчика тока ДТ и двух компараторов на блоках Relational Operator, один из которых формирует логический сигнал по условию iк > Iоп, а другой — по условию iк< –Iоп. Одновибраторы на блоках Monostable по срезам этих логических сигналов формируют импульсы Uов+ и Uов– длительностью DT (параметр, задающий для системы управления «мертвое» время), которые используются для закрытия соответствующих транзисторов в конце первого интервала полупериода. С помощью другой пары одновибраторов по срезу сигналов Uов+ и Uов– формируются задержанные на время DT сигналы Uов+з и Uов–з, которые применяются для открытия соответствующих транзисторов в начале второго интервала полупериода. Компараторы используют в качестве опорного сигнала не нулевое значение тока, а близкое к нему значение Iоп, чтобы успеть среагировать и выключить транзисторы до реального перехода тока через нуль.
Генератор импульсов Uнач формирует сигнал начала следующего полупериода с частотой 2fп и длительностью DT. По фронту этого сигнала закрываются все транзисторы инвертора, а по фронту задержанного сигнала Uнач_з открываются соответствующие транзисторы в начале первого интервала полупериода. T-триггер, который переключается в противоположное состояние по фронту импульсов Uнач, необходим для генерации логических сигналов Uнеч и Uчет, которые показывают, на каком полупериоде (нечетном или четном) работает в данный момент инвертор. Для формирования сигналов управления Uз1–Uз4 используются RS-триггеры, которые сбрасываются и устанавливаются несложными логическими схемами на элементах И (AND), ИЛИ (OR), использующими указанные выше логические сигналы управления.
Осциллограммы, снятые при пуске модели преобразователя в среде Simulink при нулевых начальных условиях в LC-контуре, представлены на рис. 12. Значения параметров модели следующие: fп = 55 кГц (Tп = 18,18 мкс), «мертвое» время равно Tп/75 = 0,24 мкс; Uвх = 35 В; Lк = 0,44 мкГн; Cк = 1,54 мкФ; Cвых = 1 мкФ; Rн = 800 Ом.
В начале переходного процесса открываются транзисторы VT1 и VT4, и формируется положительный импульс тока контура iк. После спада тока до нуля транзистор VT1 закрывается, и по истечении «мертвого» времени открывается транзистор VT2, закорачивающий вместе с транзистором VT4 резонансный контур, так что в контуре во время отрицательного импульса тока не будет источника входного напряжения uвх.
Как видно на рис. 12, первые положительный и отрицательный импульсы тока формируются так же, как и при нормальной работе схемы, однако конденсатор Ск перезаряжается во время второго импульса до отрицательного напряжения uСк, хотя при нормальной работе перезаряд происходит во время первого импульса и до положительного напряжения, в связи с этим амплитуда второго импульса больше амплитуды первого. Т. к. конденсатор перезаряжается до напряжения |uСк| > uвх + uвых/nтр, то после закрытия транзисторов VT2 и VT4 в конце отрицательного импульса открываются обратные диоды транзисторов VT2 и VT3, поэтому вместо ожидаемой паузы формируется положительный импульс тока, протекающий через источник входного напряжения в обратном направлении. Затем, после небольшой паузы после окончания указанного импульса, открываются транзисторы VT2 и VT3 и далее аналогично формируются двухполярные импульсы, но с другой полярностью, и во время паузы через обратные диоды протекает незначительный ток. Во время третьего полупериода импульсов тока вообще нет (см. рис. 12), так как в начале полупериода не выполняется условие для формирования положительного импульса тока через транзисторы VT1 и VT4 (uСк< uвх – uвых/nтр).
Также по коротким отрицательным импульсам на осциллограмме входного тока iвх во время «мертвого» времени видно, что обратные диоды в начале переходного процесса включаются и во время этого интервала. В момент времени tн ≈ 163 мкс начинается нормальная работа преобразователя с двухполярными импульсами тока, причем амплитуда первого импульса больше амплитуды второго, т. е. конденсатор Ск перезаряжается во время первого импульса тока, как и должно быть при нормальной работе схемы. В момент времени t ≈ 500 мкс процесс устанавливается, и преобразователь начинает работать в режиме с однополярными импульсами тока, как и положено при выбранных параметрах модели.
На рис. 13 представлены теоретические характеристики преобразователя в установившемся режиме и экспериментальные точки. Расчетные характеристики построены по формулам (2)–(11) с учетом значений параметров r = 21 мОм; L = Lк = 0,44 мкГн; Q = 25,45; ℵ= 0,94. Таким образом, результаты моделирования практически совпадают с результатами теоретических расчетов, представленных в работе [7].

Рис. 13. Теоретические характеристики преобразователя в установившемся режиме и экспериментальные точки
Анализ резонансного преобразователя постоянного напряжения типа LLC методом основной гармоники
Резонансные ППН, выполненные по схеме, представленной на рис. 2а, и работающие в режиме прерывистого тока в LC-контуре, когда индуктивность намагничивания трансформатора Lm по крайней мере на два порядка превышает индуктивность рассеяния LS = LS1 + L’S2, были подробно рассмотрены ранее. В настоящее время широко используются преобразователи, в которых индуктивность рассеяния соизмерима с индуктивностью намагничивания [9, 10].
Наиболее простым методом анализа и расчета таких преобразователей является метод основной гармоники [11]. Он основан на предположении о том, что передача энергии от источника входного напряжения uвх к нагрузке R через резонансный контур обусловлена первыми гармониками вызываемых в контуре напряжений и токов. Тогда ток в резонансном контуре iк полагается чисто синусоидальным. Такой подход дает близкие к точным результаты при работе с частотой выше резонансной в режиме непрерывного тока контура и весьма приближенные результаты на частотах переключений ниже резонансной (в режиме прерывного тока). Следует отметить, что при использовании метода основной гармоники многие детали работы схемы на периоде переключений будут потеряны.

Рис. 14. Схема силовой части несимметричного полумостового резонансного преобразователя (а); временные диаграммы, иллюстрирующие работу преобразователя в установившемся режиме (б)
Предположим, что каждый из транзисторов VT1, VT2 несимметричной полумостовой схемы (рис. 14а) открывается на полпериода в противофазе с другим. Выходное напряжение uи (рис. 14б) инверторного полумоста (рис. 14а) может быть представлено в виде ряда Фурье [12]
где f = 1/T — частота переключений, первая гармоника (n = 1)
Ток в резонансном контуре iк(t) предполагается синусоидальным
где Iк — действующее значение тока контура, φ — фазовый сдвиг тока относительно первой гармоники напряжения uи(1)(t).
Этот ток отстает от напряжения uи(1)(t) на угол φ > 0, если общее сопротивление контура носит индуктивный характер (индуктивный режим), когда частота переключений больше резонансной частоты контура fр, и опережает напряжение на угол φ< 0 при емкостном характере общего сопротивления контура (емкостной режим), f< fр.
Через источник входного напряжения uвх протекает входной ток iвх (рис. 14б), равный току контура на интервале T/2, когда проводит верхний транзистор VT1 (рис. 14а). В следующий полупериод входной ток равен нулю. Среднее значение входного тока определяется следующим образом:
Таким образом,
Тогда активная мощность, потребляемая от источника входного напряжения, определяется выражением
где согласно выражению (12) величина
представляет собой действующее значение первой гармоники выходного напряжения инвертора.
Диоды VD1, VD4 выходного выпрямителя открываются в момент перехода тока во вторичной обмотке трансформатора через нуль с отрицательного значения на положительное, а диоды VD2, VD3 — в момент перехода тока во вторичной обмотке через нуль с положительного значения на отрицательное. Если не учитывать ток намагничивания трансформатора im, эти моменты совпадают с моментами перехода через нуль тока iк резонансного контура. В реальной схеме отпирание диодов выпрямителя и изменение полярности напряжения на вторичной обмотке u2 происходят при переходе через нуль тока вторичной обмотки трансформатора, приведенное к первичной обмотке значение которого равно i’2 = i1 – iμ, где i1 = iк — ток в первичной обмотке трансформатора, совпадающий с током LC-контура iк. В свою очередь, изменение тока намагничивания iμ связано с напряжением u’2.
Напряжение на вторичной обмотке трансформатора u2 с учетом показанного на рис. 14б может быть представлено в виде ряда Фурье [12]
Первая гармоника этого напряжения определяется выражением
где ψ — фазовый сдвиг первой гармоники относительно напряжения uи(1)(t); выходное напряжение преобразователя uвых принимается идеально сглаженным, uвых = Uвых = const.
Полагая ток i2 синусоидальным и совпадающим по фазе с первой гармоникой напряжения на вторичной обмотке u2(1), найдем среднее значение выходного тока, совпадающее со средним значением тока нагрузки Iн.ср,
Из этого равенства получим
где I2 — действующее значение тока i2.
Из этого равенства найдем
Поскольку напряжение u2(1)(t) и ток i2(t) находятся в фазе, входное сопротивление выходного выпрямителя на частоте переключений с учетом конденсатора Cвых и сопротивления нагрузки R является чисто активным. С учетом формул (15) и (16) найдем это входное сопротивление
Имеем также очевидное равенство для выходной мощности
С учетом изложенного получаем линейную эквивалентную схему преобразователя для первых гармоник токов и напряжений (рис. 15). Здесь принята Т-образная эквивалентная схема трансформатора, в то время как во многих зарубежных работах вся индуктивность рассеяния трансформатора LS = LS1 + L’S2 считается сосредоточенной на первичной стороне и не учитываются активные сопротивления обмоток r1 и r’2 [9, 10].

Рис. 15. Эквивалентная схема преобразователя для первых гармоник токов и напряжений
Вводя относительные параметры
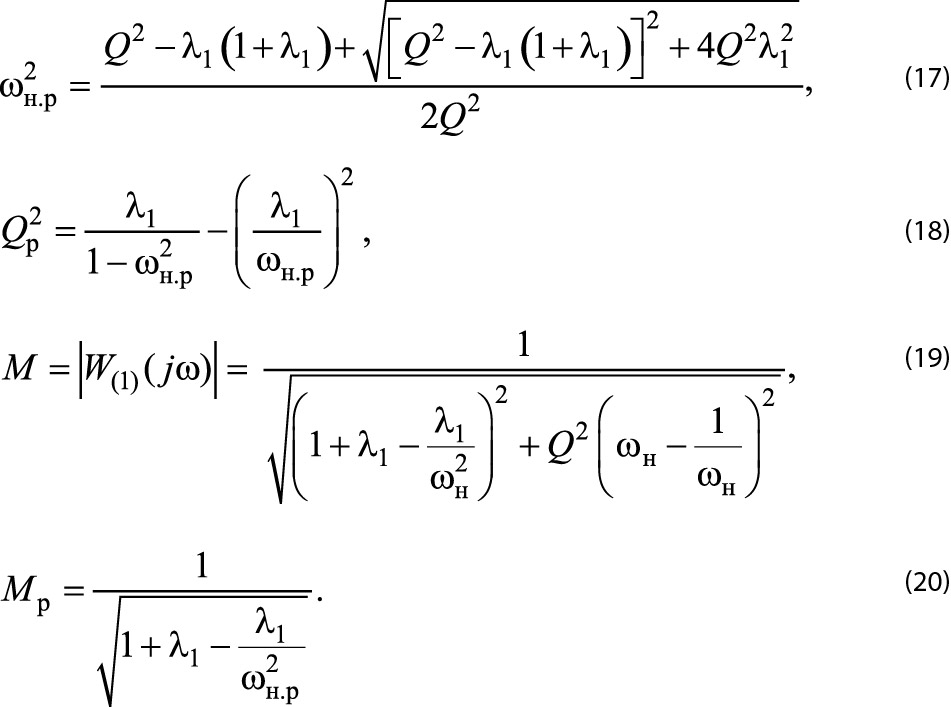
и используя эквивалентную схему (рис. 15), можно получить формулу для квадрата нормированной резонансной частоты (16.4), условие резонанса в другом виде:
формулу для модуля частотной передаточной функции (16.6) и для коэффициента передачи при резонансе
где f (r1, Q) — функция, зависящая от r1 и определяемая выражением
При допущениях, принимаемых в зарубежных публикациях, в полученных выражениях необходимо принять r1 = r’2 = 0, L’S2 = 0. Тогда получаемые выражения совпадают с известными из работы [9].
При этом получаются упрощенные формулы
Важно знать резонансную частоту, поскольку она дает границу между емкостным и индуктивным режимами LC-контура: ниже резонансной частоты комплексное сопротивление Zвх.к(jw) имеет емкостной характер, выше — индуктивный.
На рис. 16 представлены построенные по формуле (17) зависимости нормированной резонансной частоты контура w н.р от Q при различных значениях l1. Из выражения (17) следует, что при коротком замыкании нагрузки (Q → ∞) нормированная резонансная частота ω н.р = 1.

Рис. 16. Кривые для определения нормированной резонансной частоты
На рис. 17 представлены зависимости коэффициента передачи M = |W(1)(jω)| от нормированной частоты переключений ωн при различных значениях Q и постоянном λ1 = 0,2. Как видно из формулы (19), при ωн = 1 имеем M = |W(1)(jω)| = 1 независимо от значений Q. Это значение |W(1)(jω)| соответствует индуктивному характеру сопротивления контура, когда ток iк отстает по фазе от напряжения uн(1), что является необходимым условием переключений при нулевом значении напряжения на транзисторе (ПНН) [9]. В работе [9] приведены подобные зависимости также при λ1 = 0,3; 0,5; 0,9, которые показывают влияние параметра λ1 на характер этих зависимостей и могут быть использованы при выборе значения λ1 в ходе проектирования преобразователя. Максимумы этих характеристик находятся в емкостной области.
Обратим внимание на то, что коэффициент передачи M в индуктивной области уменьшается с ростом частоты w н.
График зависимости, построенной по формуле (20), для λ1 = 0,2 представлен на рис. 17 штриховой линией. Эта кривая является границей между индуктивным и емкостным режимами LC-контура: если точка (w н, M) располагается правее этой кривой, то входное сопротивление контура является индуктивным, в противном случае — емкостным.
В состоянии без нагрузки, когда R’ВХ.В → ∞, Q → 0, индуктивность LC-контура равна L1 + Lm, резонансная частота определяется выражением
а нормированная резонансная частота при холостом ходе
Для принятого на рис. 17 значения λ1 = 0,2 получим
Модуль частотной передаточной функции для рассматриваемой схемы (рис. 15) при L’s2 = 0, r’2 = 0, r1 = 0, L1 = Lk + L’s1, R’вх.в → ∞ имеет вид
Найдем КПД преобразователя
Активную входную мощность Pвх будем определять как действительную часть комплексной входной мощности
где *IK — комплексно сопряженная величина для тока İK, определяемого выражением
Величину ·Uи(1) будем полагать чисто вещественной. Тогда сопряженный ток
Выходная мощность определяется равенством
с учетом которого найдем
Поскольку
получим
Учитывая выражение
получим расчетное соотношение
В частности, при Lμ → ∞, λ1 = λ2 = 0 формула (22) преобразуется к виду
откуда с учетом выражений для –r1 и Q найдем
что легко проверить, рассматривая схему (рис. 15) при отсутствии ветви с индуктивностью Lμ. При r1 = r’2 = 0, как видно из формулы (22), h = 1.
На рис. 18 представлены зависимости, построенные по формуле (22) при r’2 = 0, λ1 = 0,2, λ2 = 0, а также экспериментальные точки, взятые из работы [10]. При этом по значениям выходной мощности, выходного напряжения Uвых = 400 В, nтр = 12, L1 = 2,2 мкГн, Cк = 0,94 мкФ, приведенным в [10], рассчитаны значения

Рис. 18. Зависимость КПД от добротности без учета потерь в выходном выпрямителе, экспериментальные токи для Uвх = 33 В, Uвых = 400 В, nтр = 12, L1 = 2,2 мкГн, Cк = 0,94 мкФ
Наши расчетные кривые на рис. 18 построены при постоянных значениях ωн, когда напряжение Uвых изменяется, поэтому вид расчетных и экспериментальных кривых различается.
Рекомендации по расчету схемы
Поскольку модуль частотной передаточной функции
где nтр = w2/w1; U’2(1) = U2(1)/nтр — приведенное к первичной обмотке действующее значение первой гармоники, напряжение на вторичной обмотке трансформатора, причем с учетом выражения (15):
Из этого равенства следует
Действующее значение первой гармоники напряжения на выходе инвертора
Отсюда следует, что
Тогда для полумостовой схемы максимальное и минимальное значения коэффициента передачи определяются выражением
где Uвх.min и Uвх.max — минимальное и максимальное значения входного напряжения.
Аналогично для мостовой схемы
При проектировании используются регулировочные характеристики для конкретных значений λ1, аналогичные представленным на рис. 17. Значение λ1 выбирается исходя из анализа семейств характеристик при различных значениях λ1. В работе [10] рекомендуется выбирать m = 6…10, что соответствует значениям λ1 = 1/(m – 1) = = 0,11…0,2.
Конструкция трансформатора, обеспечивающая заданные значения L1 и Lμ в требуемом частотном диапазоне, описана в работе [9] и показана на рис. 19.
Подставляя в левую часть уравнения (20) максимальный требуемый коэффициент передачи Mmax, получим минимальную нормированную частоту переключений
соответствующую работе преобразователя на границе между индуктивной и емкостной областями.
Подставляя выражение (23) в равенство (18), получаем максимальную добротность, позволяющую получать максимальный коэффициент передачи Mmax на границе между емкостными и индуктивными областями:
Подставив в уравнение (21) минимальный требуемый коэффициент передачи Mmin вместо M0, получим максимальную нормированную частоту переключений
Требование о том, что преобразователь должен работать в области индуктивного входного сопротивления контура (коротко, в индуктивной области), является необходимым, но недостаточным условием переключений транзистора при нулевом значении напряжения (ПНН). Влияние паразитной емкости на выходных зажимах полумоста, складывающейся из емкости сток–исток транзисторов и паразитной емкости схемы, предъявляет дополнительные требования при проектировании [9, 10].
В индуктивном режиме, показанном на рис. 20, при подаче в момент t = 0 отпирающего импульса на затвор транзистора VT1 ток контура iк отрицательный и замыкается через встроенный диод транзистора VT1, поэтому включение транзистора VT1 происходит при обратном напряжении, равном прямому падению напряжения на диоде (режим ПНН).

Рис. 20. Иллюстрация процесса переключений с учетом паразитной емкости
После окончания отпирающего импульса Uзи1 транзистор VT1 запирается, без учета паразитных емкостей положительный ток контура iк начинает замыкаться через встроенный диод транзистора VT2 и протекает по нему вплоть до отпирания транзистора VT2, обеспечивая включение транзистора VT2 при напряжении на нем, близком к нулю. В действительности после запирания транзистора VT1 имеет место короткий интервал, в течение которого оба транзистора и их встроенные диоды закрыты, пока разряжается паразитная емкость на выходном зажиме инвертора Cп. При этом справедлива эквивалентная схема, показанная на рис. 21а. Для этой схемы справедливы уравнения

Рис. 21. Схема учета паразитной емкости при включении транзистора инвертора
Согласно второму уравнению при Uвх = const справедливо равенство
с учетом которого первое уравнение преобразуется к виду
где емкость Cп = Cси1 + Cси2 учитывает не только емкость сток–исток транзисторов, но и паразитные емкости, связанные с конструкцией печатной платы. Напряжение сток–исток транзистора VT2 совпадает с выходным напряжением инвертора uи.
Когда емкость Cп разряжается до нуля, отпирается встроенный диод транзистора VT2, что подготавливает транзистор к включению при нулевом значении напряжения.
«Мертвое» время td должно превышать время разряда паразитной емкости Cп, чтобы гарантировать включение транзистора при нулевом значении напряжения на нем, т. е.
где iK(T/2) — значение тока контура в конце полупериода, которое в соответствии с выражением (13) равно √2IK sinj.
Следовательно, согласно выражению (24) необходимо выполнение условия
Из равенства (14) следует
Из последних двух соотношений получаем
Это является достаточным условием включения силовых транзисторов при нулевых значениях напряжения на них и позволяет вычислить максимальное значение добротности Qmax при максимальной выходной мощности и минимальном входном напряжении, что является громоздкой задачей. Поэтому рекомендуется воспользоваться достаточным условием включения транзисторов при нулевом напряжении, получаемом для режима холостого хода (Rвх.в → ∞) при максимальном входном напряжении [9]. В этом режиме входное сопротивление контура чисто реактивное
поэтому j = p/2. Значение тока в контуре, при котором происходит включение транзистора, с учетом (12)
поэтому с учетом (24) должно выполняться условие
Поскольку
получаем искомое неравенство
совпадающее с приведенным в работе [9].
Таким образом, учет активных сопротивлений потерь позволил получить более общие выражения для расчета основных характеристик резонансного преобразователя типа LLC. Известные из зарубежных публикаций расчетные соотношения получаются как частные случаи выражений, приведенных в статье.
На рис. 22 представлена фотография макетного образца исследуемого LLC-преобразователя.

Рис. 22. Макетный образец исследуемого LLC-преобразователя
Работа выполнена при финансовой поддержке РФФИ в рамках проекта № 15-48-02189-р_поволжье_а
- Nanosolar Commercial Solar Roof (BIPV). — Режим доступа: nanosolar.com/solutions/roof/index.html.
- Prism Solar Products. — Режим доступа: prismsolar.com/our-products/.
- Иванов А.Г., Нудельман Г.С. Силовая электроника для солнечной энергетики // Динамика нелинейных дискретных электротехнических и электронных систем (ДНДС-2013): Материалы X всерос. науч.-техн. конф. — Чебоксары: Изд-во Чуваш. ун-та, 2013. — С. 223–232.
- Белов Г. А., Серебрянников А. В., Белов С. Г. Обзор структур однофазных работающих на сеть инверторов для фотопреобразовательных модулей // Динамика нелинейных дискретных электротехнических и электронных систем: материалы XI всерос. науч.-техн. конф. Чебоксары: Изд-во Чуваш. ун-та, 2015.
- Белов Г. А., Серебрянников А. В., Павлова А. А. Анализ и расчет характеристик установившегося режима в преобразователе постоянного напряжения с последовательным резонансным инвертором // Практическая силовая электроника. № 4 (60).
- Белов Г. А. Анализ режимов преобразователя постоянного напряжения с последовательным резонансным инвертором при прерывистом токе в контуре // Практическая силовая электроника. 2016. № 1 (61).
- Белов Г. А. Расчет и анализ внешних характеристик и КПД преобразователя постоянного напряжения с последовательным резонансным инвертором при двухполярных импульсах тока на половине периода // Практическая силовая электроника. 2016. № 2 (62).
- Белов Г. А. Высокочастотные тиристорно-транзисторные преобразователи постоянного напряжения. М.: Энергоатомиздат, 1987.
- Silvio De Simone. LLC Resonant Half-Bridge Converter Design Guideline. Application Note AN2450. 2014. Режим доступа: st.com.
- Sam Abdel-Rahman. Resonant LLC Converter: Operation and Design. Application Note AN2012-09. 2012. Infineon Technologies North America (ITNA) Corp. Режим доступа: www.infineon.com.
- Забродин Ю.С. Промышленная электроника. Учеб. для вузов. М.: Высшая школа, 1982.
- Бронштейн И. Н., Семендяев К. А. Справочник по математике. М.: Наука, 1967.











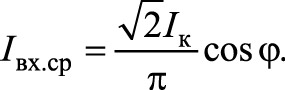

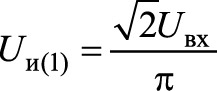




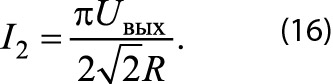











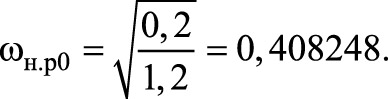
















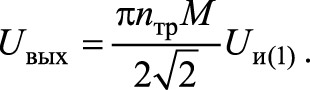


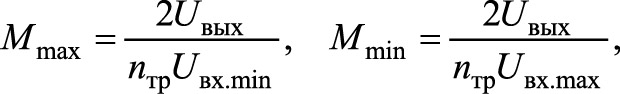










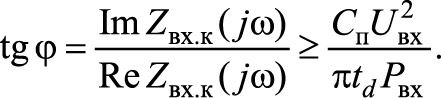
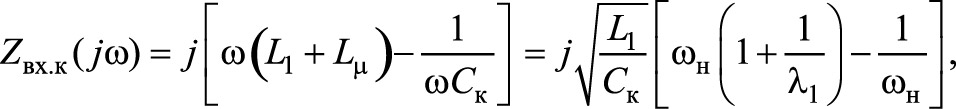



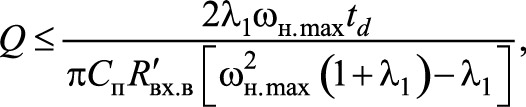
 10 июня, 2015
10 июня, 2015