
ШКОЛА MATLAB. Урок 24. Мехатронная система с магнитоэлектрическим генератором и активным полупроводниковым выпрямителем
Введение
В настоящее время в генераторных установках наблюдается повсеместный переход к синхронным машинам с постоянными редкоземельными магнитами на роторе. Такие машины проектируются и изготавливаются уже на мощности до десятков мегаватт. В отечественной литературе синхронные машины с постоянными магнитами на роторе получили название синхронных магнитоэлектрических машин (СММ). В англоязычной версии они именуются Permanent Magnet Synchronous Machine (PMSM).
При построении генераторной установки на базе СММ основная трудность заключается в поддержании постоянного напряжения на нагрузке при изменении скорости вращения машины и при изменении нагрузки. Такую задачу возможно решить при построении мехатронной системы, состоящей из машины, активного выпрямителя (АВ) и замкнутой системы управления АВ. Эта система позволяет обеспечить стабилизацию напряжения на выходе АВ при изменении скорости и нагрузки.
Функциональная схема мехатронной генераторной системы с СММ и АВ, которая рассматривается в статье, приведена на рис. 1, где блок СУАВ является системой управления АВ.

Рис. 1. Функциональная схема мехатронной системы с СММ и АВ
Математическое описание системы «СММ–АВ»
Основу активного трехфазного АВ составляет схема, представленная на рис. 2а. В этой схеме, так же как и в повышающем импульсном преобразователе [3, 4], на периоде коммутации имеют место лишь два состояния силовой цепи.

Рис. 2. Схема и структуры силовой цепи системы «СММ–АВ»
В первом состоянии (назовем его импульсом, рис. 2б) машина через соответствующие полупроводниковые ключи подсоединена к выходным зажимам АВ (к конденсатору с нагрузкой). Состояние импульса может быть реализовано при включении шести различных сочетаний силовых полупроводниковых ключей (1, 4, 6; 3, 2, 6; 5, 2, 4; 2, 3, 5; 4, 1, 5; 6, 1, 3).
Во втором состоянии (назовем его паузой) обмотки машины замкнуты накоротко. Состояние паузы реализуется при включении двух сочетаний силовых полупроводниковых ключей (1, 3, 5 или 2, 4, 6, рис. 2б). Если обозначить время существования первого коммутационного интервала через t1, а время существования второго коммутационного интервала через t2, то отношение m = t1/(t 1 + t2) называется коэффициентом модуляции.
Базой аналитических методов рассматриваемого класса систем служит теоретическое положение, разработанное А. А. Булгаковым [1, 2] и заключающееся в том, что электромагнитные и энергетические характеристики АВ определяются передачей мощности в нагрузку на основной частоте, кратной скорости вращения вала CММ. Обмен энергией между реактивными элементами осуществляется на несущей частоте переключения транзисторов в АВ. Этот обмен сопровождается пульсациями токов в системе, вызывает незначительные искажения формы токов и дополнительные (обычно незначительные) потери. Основываясь на этом положении, удается аналитически описать и исследовать некоторые характерные режимы работы АВ на основной частоте.
В основе математического описания электромагнитных процессов в системе на основной частоте лежит метод пространственного (результирующего) вектора [6, 8], позволяющий все переменные состояния представить пространственными векторами в единой системе координат. Для исследования рассматриваемой системы эту систему координат удобно связать с продольной (d) и поперечной (q) координатами синхронной машины (рис. 3), вращающимися с синхронной скоростью (w = pwm). В этом случае, как это показано на рис. 3, вектор потокосцепления возбуждения совпадает с осью d, а вектор ЭДС синхронной машины — с осью q.

Рис. 3. Система координат СММ
Математическое преобразование мгновенных значений переменных состояния системы в значения переменных состояния в осях (d, q) представлено уравнением (1) для ЭДС машины (аналогичные уравнения преобразования осуществляются для напряжений и токов).
При описании электромагнитных процессов в системе с использованием метода основной («гладкой») составляющей и метода пространственного вектора эквивалентная схема замещения СММ с АВ преобразуется к виду, представленному на рис. 4.

Рис. 4. Эквивалентная схема замещения системы «СММ–АВ»
В этой эквивалентной схеме замещения преобразователь с одной стороны подключен к статорным обмоткам СММ с ЭДС (E1), с другой — к цепи постоянного тока с нагрузкой и емкостным фильтром. Индуктивное и активное сопротивления в схеме замещения являются внутренними параметрами машины и АВ.
Математическое описание системы «СММ–АВ» на стороне переменного тока во вращающейся синхронно с валом машины системе координат может быть представлено в виде:
где –E1(t) — результирующий пространственный вектор ЭДС на статорных обмотках машины; –U1(t) — результирующий пространственный вектор напряжения АВ по основной гармонике; –I1(t) — результирующий пространственный вектор тока в якоре машины; r, x — активное и реактивное сопротивления СММ и проводящих полупроводниковых приборов АВ.
Значение ЭДС на выходе СММ определяется скоростью вращения wm вала машины и потокосцеплением возбуждения
где p — число пар полюсов в машине.
По отношению к ЭДС переменного тока, на выходе СММ активный выпрямитель генерирует напряжение, основная гармоника которого равна [7]:
где Udc(t) — напряжение в звене постоянного тока АВ; m — коэффициент модуляции; jm — фаза напряжения –U1 по отношению к ЭДС E1 на выходе машины — фаза модуляции.
Во вращающейся системе координат (d — вещественная ось и q — мнимая ось) при совмещении вещественной оси с вектором потокосцепления возбуждения СММ –Ψ0 уравнения (2, 3, 4) запишутся в виде:
Для полного описания «СММ–АВ» систему уравнений (5) следует дополнить уравнением энергетического баланса и уравнением Кирхгофа в цепи постоянного тока
где C, R — емкость конденсатора фильтра и сопротивление нагрузки.
Заметим, что запись Id(t), Iq(t), Ed(t), Eq(t), Udc(t), Idc(t) в уравнениях (5, 6) подчеркивает то обстоятельство, что эти величины являются постоянными с изменяющимися во времени значениями. Изменение значений токов, напряжения и ЭДС наблюдается во время переходных процессов.
Система уравнений (5, 6) является существенно нелинейной и не имеет аналитического решения. Исследование такой системы может быть осуществлено только при использовании современных прикладных компьютерных программ, одной из лучших среди которых является пакет MATLAB + Simulink [5]. Однако построение модели для системы уравнений (5, 6) требует некоторого предварительного качественного и количественного исследования, в котором определяется ряд физических свойств системы, ограничения на изменение ее переменных состояния, выявление областей устойчивой и неустойчивой работы (если таковые имеют место), влияние параметров на вышеперечисленные свойства и. т. д. Это, в свою очередь, требует проведения ряда частных исследований с использованием обобщенного математического описания (уравнения 5, 6). Такие исследования с последующим моделированием далее осуществляются для электрической машины PM_ZG_1322M-4A, параметры которой приведены в таблице 1.
|
P, кВт |
f, Гц |
Ef m, В |
r, Ом |
L, мГн |
J, кгм2 |
p |
|
7,5 |
50 |
310 |
0,6 |
5,9 |
10,8 |
2 |
Исследование системы «СММ–АВ» в установившемся режиме при независимом управлении
Основные физические свойства рассматриваемой системы можно выяснить, не прибегая к решению дифференциальных уравнений (5, 6) и рассматривая только установившиеся режимы работы.
В установившемся режиме работы системы уравнений (5, 6) преобразуются к виду:
Уравнения (7, 8) позволяют рассчитать и построить напряжение на выходе АВ при независимом управлении полупроводниковым преобразователем, когда управляющими величинами являются коэффициент модуляции m и фаза модуляции jm.
Основная статическая характеристика, представляющая собой зависимость выходного напряжения в звене постоянного тока АВ, определяется на основании совместного решения уравнений (7, 8).
где R — сопротивление нагрузки, z = √r2+x2 — полное сопротивление СММ и АВ на стороне переменного тока.
Из уравнений (7, 8, 9) рассчитываются электромагнитные и энергетические характеристики системы «СММ–АВ» в установившемся режиме работы:
Диапазон допустимых изменений управляющих воздействий на систему при независимом алгоритме управления АВ следует исследовать в трехмерном пространстве. Программа для построения этих характеристик представлена в листинге 1.
Листинг 1
r=0.6;
R=35;
p=2;
wm=150;
[m,fi1]=meshgrid([0:0.01:1.0]);
fi=fi1.*2;
Eq=p*wm.*310./314;
x=p*wm.*0.0059;
z=sqrt(r.^2+x.^2);
a=(3/4)*m.*(Eq.*R./z^2).*(r*cos(fi)+x.*sin(fi));
b=1+(3/8).*(m.^2).*(r*R)./z^2;
Udc=a./b;
Ud=(m.*Udc).*sin(fi)/2;
Uq=(m.*Udc).*cos(fi)/2;
Id=((r.*Ud)+x.*(Eq-Uq))./z^2;
Iq=(Eq-Uq).*r./z^2+(Ud.*x)./z^2;
P1=(1.5*Eq).*Iq;
Pdc=(Udc.^2)./R;
n=Pdc./P1;
meshc(m,fi,Udc);
grid on;
xlabel('m');
ylabel('fi (rad)');
zlabel('Udc (V)');
На рис. 5, 6, 7 показаны поверхности выходного напряжения при изменении коэффициента модуляции и фазы модуляции для трех скоростей вращения вала машины. Проекции этих поверхностей на основную плоскость представляют собой линии постоянного напряжения на выходе АВ. По этим линиям можно судить о зависимостях между коэффициентом и фазой модуляции при Udc = const. Области допустимых значений коэффициента модуляции и фазы модуляции лежат на линиях постоянного напряжения. Для выбранной (табл. 1) машины значение напряжения в звене постоянного тока при номинальной скорости вращения ее вала следует принять равным Udc = 600 В. На рис. 5, 6, 7 этому напряжению соответствуют зависимости между m и jm, выделенные жирными кривыми. Эти зависимости показывают:
- поддержание Udc=600(В) = const осуществляется, в основном, за счет изменения фазы модуляции, и только при незначительных значениях jm — за счет увеличения коэффициента модуляции;
- диапазон изменения коэффициента модуляции при Udc=600(В) = const значительно ограничен.

Рис. 5. Выходное напряжение при изменении коэффициента и фазы модуляции для wm = 100 рад/с

Рис. 6. Выходное напряжение при изменении коэффициента и фазы модуляции для wm = 150 рад/с

Рис. 7. Выходное напряжение при изменении коэффициента и фазы модуляции для wm = 200 рад/с
Аналогичные зависимости наблюдаются и при изменении нагрузки. На рис. 8 эти зависимости построены для сопротивлений нагрузки R = 35 Ом, что, по сравнению с характеристикой (рис. 6), соответствует удвоенной мощности. Здесь также по проекциям напряжения на основную плоскость определяются ограничения на диапазон изменения сигналов управления.

Рис. 8. Выходное напряжение при изменении коэффициента и фазы модуляции
Исследование системы «СММ–АВ» в установившемся режиме при токовом управлении
При независимом алгоритме управления АВ может обеспечить заданные требования к системе «СММ–АВ» с изменяющейся скоростью и сопротивлением нагрузки при реализации нелинейной зависимости m = f(jm). Причем требуемая зависимость m = f(jm) изменяется при изменении скорости и нагрузки, что делает невозможной (или очень сложной) практическую реализацию такого управления.
Поэтому при построении схемы управления АВ, рассчитываемого на работу с изменяющимися скоростью и сопротивлением нагрузки, приходится отказываться от независимого алгоритма управления и использовать управление током АВ. В этом случае управление организуется в синхронно вращающейся системе координат (d, q), с релейной отрицательной обратной связью по составляющим Id, Iq. Такое управление получило название «токового коридора».
Решающе важными для построения модели с токовым управлением являются вопросы, связанные с ограничениями. Эти ограничения определяются физическими процессами в схеме, они позволяют определить диапазон изменения задающих токовых сигналов, при которых система остается работоспособной. При токовом управлении коэффициент модуляции и фаза модуляции генерируются самой системой, однако ограничения на их значения остаются такими же, которые получены при исследовании АВ с независимым алгоритмом управления. Это ограничивает величину и диапазон изменения задающих токовых сигналов.
Дальнейшее исследование установившихся процессов осуществим, опираясь на векторные диаграммы. При построении векторных диаграмм следует учитывать, что АВ описывается в системе координат x, y (уравнение 4), связанных с напряжением Udc коэффициентом и фазой модуляции m, jm, а СММ — в системе координат d, q, связанных с потокосцеплением возбуждения и, соответственно, с ЭДС. В установившемся режиме эти системы координат вращаются синхронно, но сдвинуто на угол, равный фазе модуляции. Векторные диаграммы в синхронно вращающихся системах координат для трех выбранных режимов работы системы, построенные по уравнениям (5), показаны на рис. 9.

Рис. 9. Векторные диаграммы системы «СММ–АВ»
Векторные диаграммы позволяют оценить свойства всей системы и на этом основании выбрать оптимальный способ управления АВ. На рис. 9а показана векторная диаграмма для общего случая, когда задающие сигналы могут формироваться как в осях (x, y), так и в осях (d, q). На рис. 9б показана векторная диаграмма, когда задающие токи формируются в осях (x, y) так, чтобы реактивная составляющая была бы равна нулю (Ix = 0). В этом случае АВ вместе с нагрузкой потребляет от генератора только активную мощность. На рис. 9в показана векторная диаграмма, когда задающие токи формируются в осях (d, q) так, чтобы реактивная составляющая тока в машине была бы равна нулю Id = 0. В этом случае от машины потребляется только активная мощность, а АВ генерирует отрицательную (емкостную) реактивную мощность, которая компенсирует реактивную мощность, обусловленную реакцией якоря машины.
Далее рассматриваются свойства системы при последнем способе управления.
В диапазоне допустимых изменений задающего сигнала Iq* напряжение на выходе АВ при токовом управлении определяется из уравнения (6):
Расчет напряжения на выходе АВ осуществляется программой, приведенной в листинге 2.
Листинг 2
r=0.6;
R=70;
p=2;
[wm,Iq]=meshgrid([10:1:300]);
Eq=(310/314)*p*wm;
Iq1=Iq./10;
Udc=sqrt((1.5*Eq.*Iq1-1.5*r*(Iq1.^2)).*R);
P1=(1.5*Eq).*Iq1;
Pdc=(Udc.^2)./R;
n=Pdc./P1;
meshc(Iq1,wm,Udc);
grid on;
xlabel('Iq (A)');
ylabel('wm (1/s)');
zlabel('Udc (V)');
При найденных значениях Udc энергетические характеристики рассчитываются по уравнениям (11).
Результаты моделирования представлены на рис. 10 и 11. Кривые постоянного напряжения на выходе АВ находятся как проекции поверхности на основную плоскость. Жирными линиями отмечены зависимости при Udc = 600 В.

Рис. 10. Выходное напряжение при изменении заданного тока и скорости (R = 35 Ом)

Рис. 11. Выходное напряжение при изменении заданного тока и скорости (R = 70 Ом)
По этим зависимостям определяются ограничения на диапазон изменения скорости вращения вала машины и задающего тока, которые должны быть предусмотрены при проектировании системы управления.
Для системы с выбранными параметрами при мощности на выходе, равной 10 кВт (R = 35 Ом), эти ограничения соответствуют току 17,5 А и скорости 110 рад/с (рис. 10). Для мощности на выходе, равной 5 кВт (R = 70 Ом), эти ограничения соответствуют току 8 А и скорости 60 рад/с (рис. 11).
Модельное исследование замкнутой по напряжению системы
Блок-схема системы «СММ–АВ» при токовом управлении приведена на рис. 12. В ней на входе регулятора тока предусматривается ограничение тока, найденное из предварительного анализа (рис. 10 и 11).
Динамические свойства системы «СММ–АВ» при токовом управлении определяются на основании второго уравнения системы (6), в котором необходимо установить связь между значением тока в цепи машины и током Idc(t), заряжающим конденсатор. Заряд конденсатора постоянным напряжением связан с потреблением активной мощности из сети в течение переходного процесса. При совмещении оси q с вектором ЭДС машины активная мощность определяется током Iq(t), откуда следует, что в переходном режиме, при заряде конденсатора, имеет место равенство Idc(t) = I*q(t), этот ток и заряжает конденсатор. С учетом сказанного динамические свойства системы с токовым управлением при заряде конденсатора описываются уравнением
где I*q(t) — заданный активный ток.
Для стабилизации выходного напряжения активного выпрямителя канал управления активным током Iq включается в контур стабилизации напряжения в звене постоянного тока АВ. При этом контур напряжения строится как внешний по отношению к контуру активного тока. Во внешнем контуре стабилизации напряжения использован ПИ-регулятор, параметры которого для звена, описываемого уравнением (13), определяются по стандартной процедуре.
Структурная модель, которая позволяет исследовать электромагнитные и динамические характеристики системы «СММ–АВ» при задании напряжения в звене постоянного тока и раздельном управлении по проекциям тока в сети Id и Iq, представлена на рис. 13. Электромагнитная часть модели на стороне переменного тока описывается двумя первыми уравнениями системы (5). В блоке Subsystem1 (рис. 13) модели реализованы уравнениями (6), описывающими АВ вместе с цепью постоянного тока. Релейные регуляторы тока Id и Iq по осям d и q обеспечивают токовое управление АВ.

Рис. 14. Структурная модель блока Subsystem1
Переходные процессы по активному току и напряжению на выходе АВ при изменении нагрузки в момент t = 0,3 с и изменении скорости в момент t = 0,4 c приведены на рис. 15.

Рис. 15. Результаты моделирования структурной модели
Виртуальная модель системы представлена на рис. 16.
Эта модель позволяет исследовать не только динамические характеристики системы «СММ–АВ», но и электромагнитные, и энергетические характеристики при задании напряжения на выходе АВ (в звене постоянного тока) и раздельном управлении по проекциям токов Id и Iq.
Переходные процессы при скачкообразном изменении скорости от 100 до 150 1/с при неизменном сопротивлении нагрузки R = 70 Oм показаны на рис. 17, где представлены мгновенные токи в фазах машины, активный ток в машине Iq во вращающейся системе координат и напряжение на выходе АВ.

Рис. 17. Переходные процессы при скачкообразном изменении скорости от 100 до 150 1/с при неизменном сопротивлении нагрузки R = 70 Oм
Аналогичные переходные процессы при скачкообразном изменении нагрузки R = (70–35) Oм и постоянной скорости 150 1/с показаны на рис. 18. Обратившись к рис. 10 и 11, нетрудно заметить, что значения тока и скорости лежат на соответствующих кривых и не выходят за ограничивающие пределы, что свидетельствует о совпадении результатов моделирования с результатами аналитических расчетов характеристик.

Рис. 18. Переходные процессы при скачкообразном изменении нагрузки R = (70–35) Oм и постоянной скорости 150 1/с
Иная картина переходных и установившихся процессов наблюдается при превышении ограничений, рассчитанных по статическим характеристикам. Такой пример работы системы показан на рис. 19. Здесь при нагрузке в 35 Ом (P1 ≈ 10 кВт) в системе наблюдаются нелинейные колебательные процессы при уменьшении скорости от 150 до 100 рад/с. Обратившись к характеристикам (рис. 10), можно заметить, что при скорости wm ≈ 110 рад/с система утрачивает свои управляющие свойства.

Рис. 19. Переходные процессы при выходе системы из области ограничения
Заключение
Система «СММ–АВ» («синхронная магнитоэлектрическая машина — активный выпрямитель») является нелинейной динамической системой с дискретно изменяющимися параметрами и регулируемым эффектом накопления энергии. Всестороннее исследование ее электромагнитных и электромеханических свойств в установившемся режиме позволяет оценить энергетические возможности системы и ограничения на диапазон изменения управляющих воздействий.
Задача исследования динамических свойств системы в обобщенном теоретическом плане при независимом управлении остается открытой. При токовом управлении эти исследования для конкретных применений, как это продемонстрировано в статье, могут быть осуществлены с использованием структурных и виртуальных моделей, в которых учтены как линейные, так и нелинейные свойства системы.
- Булгаков А. А. Основы динамики управляемых вентильных систем. М.: Изд-во АН СССР, 1963.
- Булгаков А. А. Новая теория управляемых выпрямителей. М.: Наука, 1970.
- Герман-Галкин С. Г. ШКОЛА MATLAB. Урок 12. Исследование импульсного повышающего регулятора постоянного напряжения // Силовая электроника. 2010. № 1.
- Герман-Галкин С. Г. ШКОЛА MATLAB. Урок 17. Динамические режимы работы импульсного повышающего преобразователя // Силовая электроника. 2013. № 4.
- Дьяконов В. П. MATLAB 6/6.1/6.5 + Simulink 4/5. Основы применения. Полное руководство пользователя. М.: СОЛОН-Пресс, 2002.
- Ковач К. П., Рац И. Переходные процессы в машинах переменного тока. Пер. с нем. М.-Л.: Госэнергоиздат, 1963.
- Розанов Ю. К. Силовая электроника. М.: Издательский дом МЭИ, 2007.
- Park R.H. Two-reaction theory of synchronous machines: Generalized method of analysis – part 1. Trans. of AIEE. July, 1929.






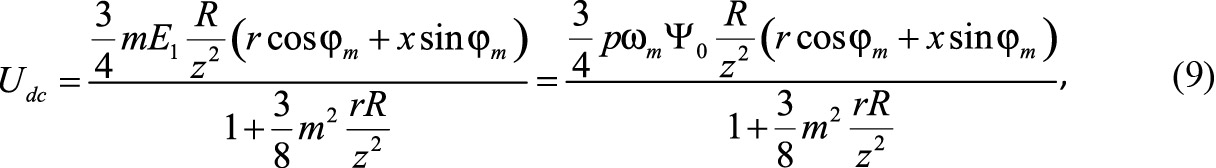


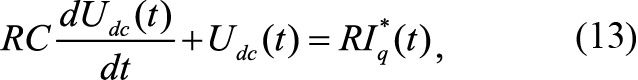


 5 сентября, 2011
5 сентября, 2011 19 сентября, 2007
19 сентября, 2007 19 февраля, 2014
19 февраля, 2014