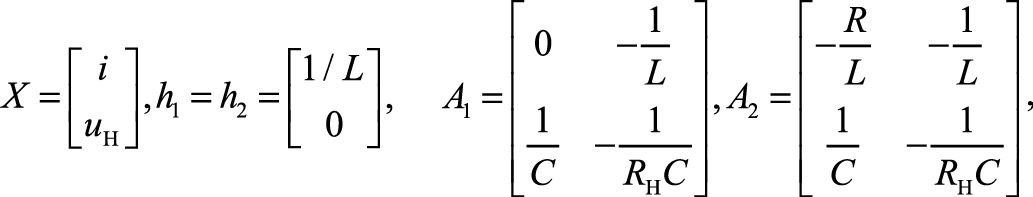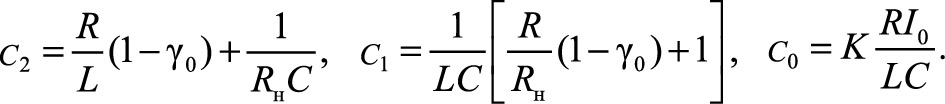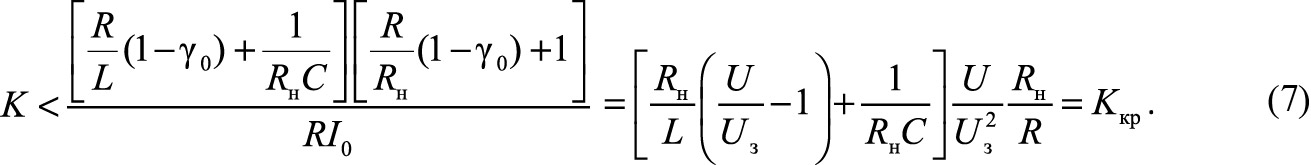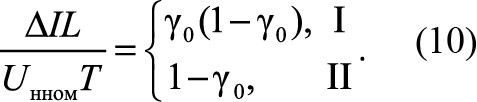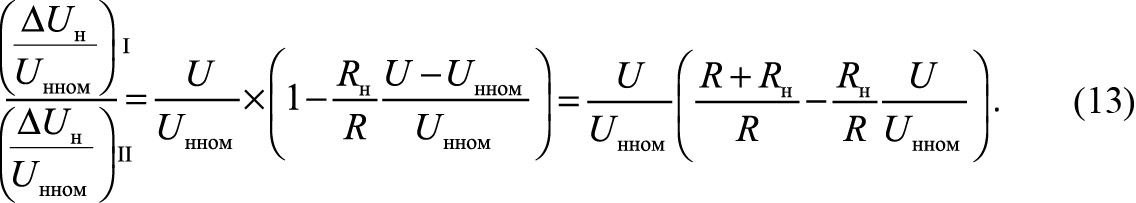Стабилизатор напряжения с параметрическим управлением

Введение

В подавляющем большинстве систем автоматического управления (САУ) информация и управляющие воздействия — это электрические напряжения и токи, механические линейные и угловые перемещения, световые и электромагнитные сигналы и т. д. В некоторых САУ сигналы и управляющие воздействия изменяют параметры устройства (элемента САУ). Например, электромеханический преобразователь, состоящий из приводного двигателя постоянного тока и синхронного генератора, осуществляет превращение напряжения постоянного тока в напряжение переменного. При этом стабилизация частоты переменного тока производится путем стабилизации частоты вращения приводного двигателя. При жестких требованиях к габаритам преобразователя, обычно применяемого на подвижных объектах, а также при мощности не более нескольких единиц киловатт стабилизация частоты вращения происходит по цепи возбуждения в результате короткого замыкания резистора, включенного последовательно с обмоткой возбуждения приводного двигателя параллельного возбуждения. При повышении скорости, вызванном сбросом нагрузки генератора, центробежный регулятор замыкает резистор, а при снижении скорости, вызванном повышением нагрузки, резистор подключается в цепь обмотки возбуждения.

Несмотря на определенные недостатки такого способа стабилизации частоты, в рассматриваемых условиях он оказался наиболее технически рациональным.

Параметрическое управляющее воздействие может оказаться предпочтительным и в других случаях. Изменяя сопротивление резистора, включенного последовательно с нагрузкой, можно регулировать напряжение на нагрузке, например стабилизировать его. Чтобы плавно изменять сопротивление резистора от нуля до номинального, нужно варьировать относительное время его короткого замыкания, осуществляющегося с высокой частотой. Подобный подход применялся в работе [1] для плавного изменения емкости конденсаторов. Разумеется, между коммутируемым резистором и нагрузкой должен быть включен сглаживающий LC-фильтр. В данной статье приведены результаты исследования стабилизатора напряжения постоянного тока с параметрическим управляющим воздействием.

Математическое описание стабилизатора напряжения

Стабилизатор напряжения постоянного тока (рис. 1) состоит из импульсного регулятора сопротивления резистора R и LC-фильтра. Ключ K периодически с высокой частотой (f = 1/T) замыкает резистор R, изменяя среднее значение сопротивления R_ср = (1 – γ)R, γ = t/T от 0 при γ = 1 до R при γ = 0.

Рис. 1. Схема стабилизатора напряжения с параметрическим управлением

Высокая частота переключений ключа К позволяет рассматривать предельную непрерывную модель стабилизатора [2]. Чтобы ее получить, запишем уравнения схемы при двух положениях ключа К:

Записав уравнения в векторной форме [2]:

где

получаем уравнение предельной непрерывной модели схемы:

где

С учетом интегрального регулятора величины γ согласно уравнению (1) получаем систему уравнений предельной непрерывной модели стабилизатора напряжения:

где K — коэффициент преобразования интегрального регулятора, U_з — заданное значение напряжения нагрузки.

Полагая U_з и U постоянными, а левые части уравнений системы (2) равными 0, получаем уравнения стационарного режима:

Из системы уравнений (3) находим:

Легко проверить совпадение первых двух уравнений предельной непрерывной модели стабилизатора (2), полученной аналитически, с уравнениями непрерывной модели схемы (рис. 2), полученной из исходной схемы (рис. 1) заменой коммутируемого резистора R эквивалентным резистором со «средним» значением сопротивления (1 – γ)R.

Рис. 2. Непрерывная модель стабилизатора напряжения

Для оценки устойчивости стационарного режима необходима линеаризованная система уравнений возмущенного движения. Подставив в систему уравнений (2): i = I₀ + di, u_н = U_н0 + du_н, γ = γ₀ + dγ, где di, du_н и dγ — отклонения от стационарного режима (возмущения), учитывая уравнения стационарного режима (3) и линеаризовав уравнения для малых возмущений, получаем линеаризованное векторное уравнение возмущенного движения:

δdX/dt = BδX,

где

δX^T = (X – X₀)^T = [δi, δu_н, δγ]^T, X₀ = [I₀, U_н0, γ₀]^T,

Для асимптотической устойчивости стационарного режима с точностью до критического случая необходимо и достаточно отрицательных вещественных частей корней характеристического уравнения [3]:

det(zE – B) = 0,            (5)

где E — единичная матрица.

Вычисление определителя (5) приводит к кубическому характеристическому уравнению:

z³ + c₂z² + c₁z + c₀=0,                (6)

где

Воспользовавшись критерием устойчивости Вышнеградского [4], получаем условие асимптотической устойчивости в виде неравенства

Из формулы (7) очевидно, что критический коэффициент K_кр возрастает при увеличении U.

Для сравнения рассмотрим стабилизатор напряжения на понижающем импульсном преобразователе напряжения постоянного тока (рис. 3).

Рис. 3. Cтабилизатор напряжения на понижающем импульсном преобразователе

Записав дифференциальные уравнения силовой части схемы для двух положений ключа К, получаем:

Переписав эти уравнения в векторной форме

где

согласно работе [2] получаем уравнения предельной непрерывной модели, оказавшиеся линейными,

dX/dt = AX + hγU.                 (8)

С учетом уравнений (8) и интегрального регулятора γ получаем систему линейных уравнений стабилизатора напряжения:

Стационарный режим, найденный из уравнений (9), определяется выражениями

Уравнения возмущенного движения совпадают с уравнениями (9):

а в векторной форме с уравнением

где

Характеристическое уравнение возмущенного движения имеет вид:

где c₂ = 1/R_нC, c₁ = 1/LC, c₀ = KU/LC.

Согласно критерию Вышнеградского, необходимое и достаточное условие устойчивости стационарного режима выражено неравенством

Сравнение основных свойств стабилизатора при параметрическом управлении со свойствами стабилизатора, использующего понижающий импульсный преобразователь

Ограничим сравнение случаем использования стабилизаторов во вторичных источниках питания, где колебания стабилизируемого напряжения относительно невелики, а требования к стабильности выходного напряжения высоки. Зададим колебание входного (стабилизируемого) напряжения ограниченным 20% в сторону снижения. Примем минимальное входное напряжение равным номинальному выходному, пренебрегая сопротивлением замкнутого ключа К. Тогда

U_min = U_{н ном}, U_max = 1,25U_{н ном},

ΔU = U_max – U_min = 0,25U_{н ном}.

Требования по допустимому току транзисторного ключа в обоих стабилизаторах одинаковы. Во втором стабилизаторе необходим еще и обратный диод VD с таким же допустимым током. По допустимому напряжению в первом стабилизаторе транзисторный ключ выбирается исходя из напряжения 0,25U_{н ном}. Во втором же стабилизаторе транзисторный ключ и обратный диод выбираются по допустимому напряжению 1,25U_{н ном}, то есть в 5 раз большему.

Чтобы сравнить переменную составляющую напряжения на входе фильтра (u_ф на рис. 1, 3) в обоих стабилизаторах, пренебрежем пульсациями тока, а транзисторные ключи и диод примем идеальными. На  рис. 4а представлена переменная составляющая u_ф в первом стабилизаторе при 1,125U_н. С учетом R = 0,25R_н согласно формуле (4) получаем γ = 1 – 4 × 0,125 = 0,5.

Рис. 4. Переменные составляющие напряжения на входе фильтра:
а) в стабилизаторе с параметрическим управлением;
б) в стабилизаторе с импульсным понижающим преобразователем

На рис. 4б представлена переменная составляющая u_ф во втором стабилизаторе (γ₀ = 1/1,125 = 0,8).

Из рис. 4а, б будет очевидно, что размах пульсаций входного напряжения фильтра ΔU_ф = U_{ф max} – U_{ф min} в первом стабилизаторе оказался значительно меньше, чем во втором. Если во втором ΔU_ф = U, а изменяется в пределах от U_min до U_max, то в первом размах пульсаций ΔU_ф = I_н0R = U_н0R/R_ном = 0,25U_{н ном} и не изменяется. Это утверждение не распространяется на граничные точки: γ₀ = 0 и γ₀ = 1 (U = U_max и U = U_min).

Пренебрегая пульсациями тока (iR = const) и напряжения на нагрузке (U_н = const), полагаем, что переменная составляющая u_ф полностью падает на дросселе фильтра с индуктивностью L. Это позволяет считать, что в стационарном режиме за первую часть периода коммутации (0< t< t) ток дросселя i увеличивается на ΔI = (U – U_{н ном})t/L, а во второй его части (t< t< T) уменьшается на эту же величину ΔI. Нетрудно получить выражение для ΔI в первом (I) и втором (II) стабилизаторах:

Полагая, что пульсирующая (переменная составляющая тока i) замыкается только через конденсатор фильтра, найдем размах пульсаций выходного напряжения. Учитывая пилообразный характер пульсаций тока с нулевыми точками в середине частей периода, получаем

Интеграл в формуле (11) вычислен как площадь треугольника с высотой DI/2 и основанием T/2.

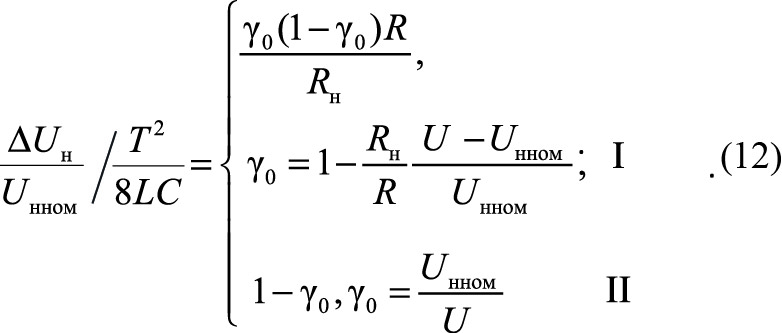
С учетом формул (10) и (11) получаем размах пульсаций выходного напряжения в первом (I) и втором (II) стабилизаторах

Соотношение относительного размаха пульсаций выходного напряжения первого (I) и второго (II) стабилизаторов напряжения при одинаковых параметрах фильтра определяет выражение

Из формулы (13) следует, что отношение размахов пульсаций первого и второго стабилизаторов при увеличении U от U_min до U_max уменьшается от 1 до 0. Максимальный относительный размах пульсаций первого стабилизатора имеет место при γ₀ = 1/2(U/U_{н ном} = = R/2R_н + 1 = 1,125) и составляет ΔU_н/U_{н ном} = = (T²/8LC)R/4R_н. По сравнению с таковым у второго стабилизатора, имеющим место при γ₀ = U_{н ном}/U_max и равным

ΔU_н/U_{н ном} = (T²/8LC)(U_max – U_min)/U_{н ном} = (T²/8LC)R/R_н,

оказывается в 4 раза меньше. Следовательно, для одинакового максимального размаха пульсаций ΔU_н/U_{н ном} второй стабилизатор должен иметь произведение LC в 4 раза большее. При этом дроссель фильтра следует рассчитывать при значительно больших пульсациях напряжения на нем, чем у первого стабилизатора.

Недостатком первого стабилизатора являются потери в резисторе, используемом для регулирования напряжения. Для сравнения КПД двух стабилизаторов примем ключи, диод, дроссель и конденсатор идеальными, то есть учтем только потери в резисторе R. Очевидно, что в этом случае КПД второго стабилизатора   = 100%. У первого же КПД изменяется в зависимости от величины U. При U = U_max h = h_min = (R_н/(R_н + R)) × 100%, а при U = U_min h = h_max = (R_н/R_н) × 100% = 100%.

В случае U_min< U< U_max КПД имеет значение

Исследование стабилизатора с параметрическим управлением методом математического моделирования

Для примера рассчитаем стабилизатор с параметрическим управлением при U_{н ном} = 100 В, 100 В < U < 125 В, I_{н ном} =1 А (R_н = 100 Ом).

При U = U_max избыток напряжения гасится на сопротивлении R. Полагая γ₀ = 0, при U = U_max получаем

Выберем частоту коммутации 5 кГц (T = 0,0002 c). Задав допустимый размах пульсаций тока ΔI < 65 мА (6,5×10^–3 А), согласно формуле (10) выбираем индуктивность дросселя, приняв γ₀ = 0,5, что соответствует максимуму ΔI:

Величину емкости конденсатора фильтра определим по допустимому размаху пульсаций выходного напряжения ΔU < 16 мB. Используя формулу (12), находим, приняв γ₀ = 0,5,

Согласно формуле (7) при выбранных значениях R, L, C и γ = γ₀ = 0,5 определяем критический коэффициент преобразования интегрального регулятора

Чтобы проверить полученные результаты в системе MATLAB 6.5, с помощью пакета Simulink 5 были построены предельная непрерывная модель стабилизатора по дифференциальным уравнениям (2) и дискретная модель, учитывающая коммутацию резистора R (рис. 5).

Рис. 5. Непрерывная и дискретная модели стабилизатора

Для U = 112,5 B (γ₀ = 0,5), K = 10 1/B^.c, соответствующем запасу устойчивости 20lg(32,6/10) = 10 дБ, построен переходный процесс включения стабилизатора. На рис. 6 представлены кривые изменения фазовых координат непрерывной (i_н, u_нн, γ_н) и дискретной модели (i_д, u_нд, γ_д).

Рис. 6. Переходный процесс включения стабилизатора

Фазовые координаты обеих моделей практически совпадают, заметна только пульсационная составляющая тока дискретной модели. Там же показаны пульсации тока и напряжения в увеличенном масштабе. Расчетные значения пульсаций ΔU_н = 16 мB и ΔI = 62,5 мA хорошо согласуются со значениями, определенными в результате моделирования: ΔU_н = 15,5 мB, ΔI = 63,7 мA.

К превышению критического коэффициента интегрального регулятора приводят автоколебания стабилизатора, являющегося нелинейной системой не только вследствие умножения фазовых координат i и γ в первом уравнении системы (2), но и в результате ограничения величины выходного сигнала интегрального регулятора диапазоном 0< γ< 1.

При K = 40 1/B^.c размах колебаний выходного напряжения составляет 17 В при периоде колебаний 8,31×10^–3 c. В автоколебательном режиме проявляется ограничение γ снизу на уровне 0.

Выводы

Параметрическое управление, основанное на изменении эквивалентного сопротивления коммутируемого резистора, имеет определенные преимущества по сравнению с применением импульсного понижающего преобразователя при использовании обоих способов в стабилизаторах напряжения вторичных источников питания.

Его основные преимущества:

• значительно более легкие условия работы транзисторного ключа и отсутствие обратного диода;
• максимальные пульсации выходного напряжения при одинаковом произведении параметров фильтра LC будут в 4 раза меньше при параметрическом управлении, а кроме того, максимальное переменное напряжение на дросселе также будет существенно ниже.

Основной недостаток рассмотренного параметрического управления — снижение коэффициента полезного действия вследствие потерь в резисторе.

Анализ свойств стабилизатора по его предельной непрерывной модели дает результаты, хорошо согласующиеся с полученными на дискретной модели при вполне реальных частотах коммутации.