Школа MATLAB. Урок 19. Переходные процессы в параллельном активном фильтре
Введение
Теория мгновенной мощности [1, 2] позволяет определить активные и неактивные электромагнитные составляющие в несимметричных и нелинейных трехфазных электрических цепях и на этой основе составить математическое описание алгоритма управления активным фильтром, при котором обеспечивается компенсация всех неактивных составляющих полной мощности. При реализации рассчитанного алгоритма управления активным фильтром коэффициент мощности (PF — power factor) для электрической системы переменного тока становится близким к единице.
Функциональная схема трехфазной сети с параллельным активным фильтром представлена на рис. 1. Принципиальная схема такого фильтра и ее описание приведены в работе [4]. Полная мощность трехфазной активно-реактивной, нелинейной и несимметричной нагрузки складывается из активной мощности ( ![]() ), неактивной пульсирующей мощности (
), неактивной пульсирующей мощности (![]() ), реактивной мощности смещения (
), реактивной мощности смещения ( ![]() ) и реактивной пульсирующей мощности (
) и реактивной пульсирующей мощности (![]() ) [1].
) [1].

Рис. 1. Функциональная схема трехфазной сети с активным фильтром
Активные фильтры генерируют всю гамму неактивных составляющих мощности в нагрузку и тем самым на 20–25% уменьшают загрузку питающих линий и генерирующих систем [10]. Ниже рассматривается трехфазный параллельный активный фильтр (АФ), предназначенный для генерации реактивных токов в симметричной трехфазной активно-индуктивной нагрузке. При этом разработана методика анализа динамических процессов в АФ, базирующаяся на совместном рассмотрении электромагнитных переходных процессов, квазиустановившихся процессов и переходных коммутационных процессов.
Анализ электромагнитных процессов в сети с активным фильтром
Синтез алгоритма управления, обеспечивающего генерацию активным фильтром реактивных составляющих токов нагрузки, решается путем адекватного преобразования координат. Основные системы координат и их свойства, которые используются при математическом описании электромагнитных процессов в трехфазных электрических цепях, приведены в табл. 1 [6].
|
Система координат |
Число осей |
Угол между осями, град |
Поведение осей |
|
Плоскость |
|||
|
abc |
3 |
120 |
Неподвижные |
|
ab |
2 |
90 |
Неподвижные |
|
dq |
2 |
90 |
Вращающиеся |
|
Пространство |
|||
|
ab,0 |
3 |
90 |
Неподвижные |
|
dq,0 |
3 |
90 |
Вращающиеся |
|
pq,r |
3 |
90 |
Вращающиеся |
Классическое преобразование Парка из неподвижной системы координат (abc) во вращающуюся систему координат (dq0) требует вычисления вещественной и мнимой мгновенных мощностей с последующим выделением постоянных и пульсирующих составляющих этих мощностей, расчетов токов, соответствующих этим мощностям, и построения систем управления, обеспечивающих компенсацию неактивных составляющих этих токов [11, 12]. Все эти преобразования осуществляются для мгновенных значений токов и напряжений.
Совершенно иная задача решается при анализе электромагнитных процессов в сети с активным фильтром. Цель такого анализа — установление соотношений между действующими или амплитудными значениями переменных состояния и проведение на основании полученных соотношений расчета основных характеристик, причем как в переходных, так и установившихся режимах. Основой анализа электромагнитных процессов АФ в такой постановке является метод пространственного вектора [8] и «гладкой составляющей» [3].
При описании электромагнитных процессов с использованием метода пространственного вектора функциональная схема АФ преобразуется к виду, представленному на рис. 2. В этой схеме, являющейся частным случаем активного преобразователя [5], полупроводниковый преобразователь (ПП) с одной стороны подключен к трехфазной сети переменного тока с амплитудным напряжением (![]() ) через дроссель, с другой — к цепи постоянного тока с конденсатором. Дроссель является накопителем «кинетической» энергии, а конденсатор накапливает «потенциальную» энергию. Обмен энергией между дросселем и конденсатором осуществляется полупроводниковым преобразователем на высокой (коммутационной) частоте.
) через дроссель, с другой — к цепи постоянного тока с конденсатором. Дроссель является накопителем «кинетической» энергии, а конденсатор накапливает «потенциальную» энергию. Обмен энергией между дросселем и конденсатором осуществляется полупроводниковым преобразователем на высокой (коммутационной) частоте.

Рис. 2. Функциональная схема АФ
Со стороны сети математическое описание АФ по «гладкой составляющей» во вращающейся системе координат может быть представлено в виде [5]:
где ![]() — результирующий вектор напряжения сети;
— результирующий вектор напряжения сети; ![]() — результативный вектор противо-ЭДС АФ;
— результативный вектор противо-ЭДС АФ; ![]() — результирующий вектор тока АФ; r — активное сопротивление, учитывающее сопротивление источника, дросселя и проводящих полупроводниковых приборов АФ; L — индуктивность дросселя; x = w1L — реактивное сопротивления дросселя на частоте сети. Заметим, что амплитуды результирующих векторов напряжения, противо-ЭДС и тока зависят от времени, что подчеркивает запись их как функций времени.
— результирующий вектор тока АФ; r — активное сопротивление, учитывающее сопротивление источника, дросселя и проводящих полупроводниковых приборов АФ; L — индуктивность дросселя; x = w1L — реактивное сопротивления дросселя на частоте сети. Заметим, что амплитуды результирующих векторов напряжения, противо-ЭДС и тока зависят от времени, что подчеркивает запись их как функций времени.
По отношению к сети переменного тока АФ генерирует ЭДС, результирующий вектор которой равен [9]:
где Udc(t) — напряжение на конденсаторе (в звене постоянного тока); m — коэффициент модуляции; jm — фаза напряжения управляющего сигнала по отношению к напряжению сети.
Анализ квазиустановившихся электромагнитных процессов в сети с активным фильтром
Со стороны сети математическое описание АФ в квазиустановившемся режиме находится из уравнения (1):

Рис. 3. Векторная диаграмма АФ
Обычно x>>r, поэтому в дальнейшем при анализе квазиустановившихся процессов используется последнее выражение уравнения (3).
Если вектор напряжения сети ![]() совмещен с вещественной осью d, то векторная диаграмма АФ в комплексной плоскости, составленная по уравнению (3), примет вид, показанный на рис. 3. Ток сети
совмещен с вещественной осью d, то векторная диаграмма АФ в комплексной плоскости, составленная по уравнению (3), примет вид, показанный на рис. 3. Ток сети ![]() содержит активную
содержит активную ![]() и реактивную (индуктивную)
и реактивную (индуктивную) ![]() составляющие. Для того чтобы ток сети был чисто активным, ток АФ
составляющие. Для того чтобы ток сети был чисто активным, ток АФ ![]() должен компенсировать реактивную составляющую
должен компенсировать реактивную составляющую ![]() т. е. ток фильтра должен быть чисто емкостным. Из векторной диаграммы следует, что ток АФ направлен по оси q, поэтому
т. е. ток фильтра должен быть чисто емкостным. Из векторной диаграммы следует, что ток АФ направлен по оси q, поэтому ![]() Для тока фильтра, направленного по оси q, падение напряжения на индуктивном сопротивлении дросселя
Для тока фильтра, направленного по оси q, падение напряжения на индуктивном сопротивлении дросселя ![]() и противо-ЭДС
и противо-ЭДС ![]() совпадают с осью d, поэтому jm = 0.
совпадают с осью d, поэтому jm = 0.
По векторной диаграмме определяются геометрические соотношения между напряжением сети, противо-ЭДС и током АФ.
Из уравнения (4) следует принципиальный вывод о том, что для получения емкостного тока в АФ противо-ЭДС E01 должна превышать напряжение сети U1 тем больше, чем больше реактивная составляющая тока нагрузки.
Анализ электромагнитных динамических процессов при независимом управлении активным фильтром
При независимом управлении активным фильтром переменными режима (управляющими сигналами) являются коэффициент модуляции и фаза модуляции. При этом в синхронно вращающейся системе координат (d — вещественная ось и q — мнимая) при совмещении вещественной оси d с вектором напряжения сети фаза модуляции равна нулю, а уравнения (1, 2) в проекциях с учетом звена постоянного тока запишутся в виде:
где C — емкость конденсатора фильтра, Idc(t) — ток заряда конденсатора.
На основании системы уравнений (5) можно получить дифференциальное уравнение АФ относительно тока Iq(t):
Характеристическое уравнение АФ запишется в виде:
Корни характеристического уравнения (7) равны:
где t = L/r — постоянная времени.
Из уравнения (8) следует, что АФ при независимом управлении представляет собой колебательное звено, собственная частота которого равна частоте сети, а коэффициент затухания равен половине постоянной времени, определяемой параметрами АФ.
Модельное исследование активного фильтра при независимом управлении
Для построения структурной модели АФ при независимом управлении на основании системы уравнений (5) необходимо установить связь между значением тока фильтра и током Idc(t), заряжающим конденсатор.
Заряд конденсатора постоянным напряжением связан с потреблением активной мощности из сети в течение переходного процесса. При совмещении вещественной оси d с вектором напряжения сети активная мощность определяется током Id(t), откуда следует равенство Idc(t) = Id(t). Этот ток и заряжает конденсатор.
С учетом сказанного структурная модель АФ с независимым управлением, построенная в соответствии с системой уравнений (5), приобретает вид, приведенный на рис. 4.
Переходные электромагнитные процессы в АФ при m = 0,8 для фильтра с параметрами L = 0,01 Гн (x = 3,14 Ом), r = 0,1 Ом, С = 320 мкФ и с определением управляющих сигналов в системе координат dq реализованы в программной среде MATLAB-Simulink для трехфазной электрической сети с параметрами U1 = 310 В, w1 = 314 рад/c, Ir = –40 A.
Результаты этого исследования, представленные на рис. 5, подтверждают теоретические положения, полученные в уравнениях (6–8).
Анализ электромагнитных переходных процессов при токовом управлении активным фильтром
Для того чтобы параллельный активный фильтр компенсировал реактивный ток, он должен представлять собой источник тока, для реализации которого управление полупроводниковым преобразователем организуется в системе с обратной связью по току в дросселях. Такое управление будем называть токовым. В неподвижной системе координат оно осуществляется с помощью релейных регуляторов [5, 9]. Такое управление в преобразовательной технике получило название «токовый коридор», или «скользящее токовое управление». Во вращающейся системе координат в качестве регуляторов токов могут быть использованы линейные ПИД-регуляторы.
При токовом управлении ток в дросселе пульсирует с высокой несущей частотой f относительно заданного значения, которое в дальнейшем обозначается Iq*. При этом в течение периода T = 1/f образуются два коммутационных интервала. На первом интервале конденсатор через соответствующие включенные транзисторы подсоединен к сети через дроссель. На этом интервале длительностью t1 протекающий по цепи ток обеспечивает обмен реактивной энергией между дросселем, конденсатором и сетью. На втором коммутационном интервале дроссель подключен непосредственно к сети и обмен энергией осуществляется между дросселем и сетью. Длительность этого интервала обозначим через t2 = T – t1. Отношение максимальной длительности первого коммутационного интервала к периоду несущей частоты является коэффициентом модуляции m = t1/T.

Рис. 6. Схемы замещения АФ в периоде коммутации
Во вращающейся системе координат dq заданное значение тока фильтра IF = Iq* является постоянным. При этом несущая частота и длительности коммутационных интервалов также постоянны, а длительность первого коммутационного интервала равна коэффициенту модуляции.
Схемы замещения АФ на первом и втором коммутационных интервалах показаны на рис. 6а, б.
Рассмотрим электромагнитные процессы, протекающие на периоде коммутации в АФ. Дифференциальные уравнения на первом и втором коммутационных интервалах с граничными значениями тока в них запишутся в виде:
где iq — мгновенный ток АФ в периоде коммутации; DIq — амплитуда пульсации тока АФ, которая определяется постоянной времени t = L/r, шириной петли гистерезиса релейного регулятора тока и величиной заданного тока фильтра Iq = IF*.
Время существования первого коммутационного интервала определяется путем решения дифференциального уравнения (9) на этом интервале:
Время существования второго коммутационного интервала определяется решением дифференциального уравнения (9) на этом интервале:
где Ib = U1/x — ток короткого замыкания.
Следует заметить, что ток АФ не может превысить значения тока короткого замыкания, обычно Iq* ≤ (0,5 – 0,7)Ib.
Из уравнений (10, 11) определяется период несущей частоты
На рис. 7 по уравнению (12) построены зависимости периода несущей частоты от относительного тока фильтра IF(pu) = Iq*(pu) = Iq*/Ib для трех значений относительной пульсации тока DIq(pu) = DIq/Ib.
Обычно DIq на два и более порядка меньше, чем ток короткого замыкания Ib. Совместное решение уравнений (10, 11) позволяет найти замкнутое выражение для коэффициента модуляции АФ:
Модельное исследование активного фильтра при токовом управлении
Полное математическое описание динамических процессов по гладким составляющим при токовом управлении АФ находится на основании уравнений (5, 13) с учетом равенства Idc(t) = Id(t). В операторной форме это математическое описание имеет вид:
где W(s) — операторная функция ПИД-регулятора; Id* = 0 и Iq* = IF — заданные токи.
Структурная модель для исследования динамических свойств активного фильтра во вращающейся системе координат dq, построенная на основании системы уравнений (13, 14), представлена на рис. 8.
Синтез ПИД-регулятора осуществлен на технический оптимум для динамического звена, описанного уравнением (6). Переходные процессы по напряжению и току конденсатора, а также по току фильтра для АФ с параметрами L = 0,01 Гн (x = 3,14 Ом), r = 0,1 Ом, С = 320 мкФ, Iq* = 40 А, Id* = 0 А приведены на рис. 9.
Заключение
Основная цель данного урока — разработка методики анализа переходных электромагнитных процессов в параллельном активном фильтре. Она базируется на классических методах «результирующего вектора» и «методе гладкой составляющей». Данная методика базируется на совместном рассмотрении трех процессов: электромагнитных переходных, квазиустановившихся и коммутационных. Причем электромагнитные квазиустановившиеся и переходные процессы описывают изменение амплитудных значений переменных состояния в функции времени, а коммутационные процессы описывают изменения мгновенных значений переменных состояния в функции времени. Благодаря такому подходу удалось получить математическое описание активного фильтра при токовом управлении полупроводниковым преобразователем. На основе полученного математического описания АФ разработаны структурные модели для исследования динамических процессов в трехфазном активном фильтре, предназначенном для компенсации реактивного тока в трехфазной симметричной нагрузке.
- Akagi H. et al. Generalized theory of instantaneus reactive power in three-phasecircuits // Conf. Rec. IPEC’83, Tokyo, 1993.
- Akagi H. New trends in active filters // Conf. Proc. EPE’95, Sevilla, 1995.
- Булгаков А. А. Новая теория управляемых выпрямителей. М.: Наука, 1970.
- Герман-Галкин С. Г. Школа MATLAB. Урок 6 // Силовая электроника. 2007. № 4.
- Герман-Галкин С. Г. Виртуальные лаборатории полупроводниковых систем в среде Matlab-Simulink. СПб: Лань, 2013.
- Жемеров Г., Колесник В., Ильина Щ. Соотношения для преобразований координат обобщенных векторов напряжений и токов трехфазной системы электроснабжения // НТУ. «ХПИ». Харьков, 2009.
- Зиновьев Г. С. Основы силовой электроники. Ч. 2, Новосибирск, Изд-во НГТУ,
- Ковач К. П., Рац И. Переходные процессы в машинах переменного тока / Пер. с нем. М.-Л.: Госэнергоиздат, 1963.
- Розанов Ю.К. Силовая электроника. М.: Изд. дом МЭИ, 2007.
- Чаплыгин Е.Е., Калугин Н.Г. Теория мощности в силовой электронике / Учеб. пособие для студентов, обучающихся по специальности «Промышленная электроника». М.: МЭИ (ТУ),
- Kim H, Blaabjerg F., Back-Jensen B. Instentaneous power compensation in three – phase systems using p-q-r theory / IEEE Trans // Power Electronics, V.17, 2002, № 5.
- Strzelecki R., Supronowicz H. Filtracja harmonicznych w sieciach zasilających prądu przemennego Toruń; Adam Marszałek, 1998.





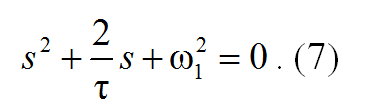



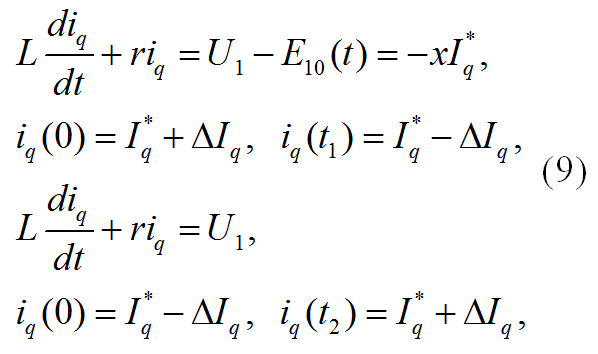

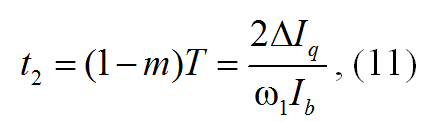






 5 сентября, 2011
5 сентября, 2011 1 мая, 2017
1 мая, 2017 28 июня, 2020
28 июня, 2020