Минимизация реактивной мощности в асинхронной короткозамкнутой машине
Электрическая машина — это многоканальный объект управления. Являясь произведением двух регулируемых величин, электромагнитный момент выступает в качестве выходной величины. Путем стабилизации одной из них управление электрической машиной приводится к одноканальной системе, что делает его достаточно простым, но значительно ограничивает возможности, уделяя внимание динамическим оценкам качества и мало затрагивая энергетические свойства, показатели которых могут наряду с электромагнитным моментом выступать как выходные величины. В связи с ростом цен на электроэнергию и ужесточением требований к экологической безопасности задача повышения энергетической эффективности работы электропривода, при высоком качестве динамических процессов, выдвигается на первый план.
Имея наиболее широкое распространение в массовом электроприводе, асинхронная короткозамкнутая машина в номинальных режимах функционирования обладает достаточно низкими потерями и наилучшим значением cos(j), характеризующим эффективность использования мощности, подводимой к обмоткам двигателя. При изменении нагрузки этот показатель значительно снижается, ухудшая эффективность применения управляющих воздействий и существенно сокращая энергетические возможности работы электрической машины. Поэтому наиболее актуальным становится сохранение средствами электропривода максимального значения cos(j) при различной нагрузке.
В рамках разработанного метода [1] рассматривается решение задачи управления асинхронной короткозамкнутой машиной, обеспечивающего изменение электромагнитного момента в условиях минимизации реактивной мощности.
Математическое описание представлено уравнениями Кирхгофа, описывающими состояния асинхронной машины в системе вращающихся со скоростью поля координат d,q (1):

где I, U — вектор тока и напряжения, подводимого к обмоткам двигателя; R — матрица сопротивлений обмоток статора и ротора; Ω — матрица величин, характеризующих скорость вращения вала двигателя ωr и поля статора ωs; p — число пар полюсов:
ωΔ = ωs – ωr.
Взаимосвязь токов и потокосцеплений определена посредством следующих уравнений:

где L — матрица индуктивностей; Lm — взаимная индуктивность обмоток статора и ротора; Ls, Lr — полные индуктивности обмоток статора и ротора; ωΔ — разность скоростей вращения поля статора и ротора двигателя определена из условий ориентации потокосцепления ротора. При ориентации системы координат по потокосцеплению ротора
Ψrq = 0, Ψrd =Ψr:

В качестве регулируемых переменных выбраны потокосцепления. Такой выбор позволит наиболее просто учесть нелинейность характеристики намагничивания при реализации системы управления, полагая, что путем измерения токов, напряжений и угловой частоты вращения ротора вектор регулируемых переменных вычисляется достаточно точно:

Выходной величиной системы управления (1) является электромагнитный момент m, значение которого определено из уравнения баланса мощностей:

P — мощность, отдаваемая двигателем исполнительному механизму; j — угол, определяет положение вектора электродвижущей силы е от потокосцепления статора Ψ относительно тока статора i и наряду с электромагнитным моментом характеризует величину реактивной мощности Q:

С помощью регулируемых переменных, путем их перемножения электромагнитный момент выражен следующим образом:

Диаграмма работы асинхронной машины с короткозамкнутым ротором представлена на рис. 1. Здесь угол b определяет положение вектора потокосцепления статора относительно потокосцепления ротора; m — угол, определяет положение вектора тока статора.
В работе ставится задача формирования вектора управления U, принадлежащего области пространства допустимых управлений, обеспечивающего перевод системы (1) из начального состояния в состояние, определенное заданным значением выходной (6) величины m за минимальное время, при одновременном регулировании реактивной мощности до своего минимального значения. Под допустимым управлением понимается все множество управлений, позволяющих сформировать предписанное значение электромагнитного момента.
Для решения поставленной задачи определена зависимость регулируемых и выходных величин:

где В — матрица коэффициентов, отражающих в пространстве состояний электрической машины (посредством варьируемого аргумента b) положение векторов, где возможно сформировать электромагнитный момент в условиях минимизации реактивной мощности:

Для выявления управления, обеспечивающего линейную зависимость электромагнитного момента от его задания, левая и правая части уравнения (4) умножены на скалярную величину потокосцепления ротора Yr :
dΨ/dt × Yr = VΨΨr + UΨr.
Это уравнение дополнено до представления полной производной:

где в соответствии с (1):

Вектор управления U сформирован таким образом, чтобы в совокупности с обратными связями по регулируемым переменным (7) он отражал задание Uref выходной величины (6) системы (1) в заданном положении вектора регулируемых величин (8), определенном элементами матрицы В [2]. Для более простого изложения материала в качестве регулятора рассматривается П-регулятор:
где K — матрица коэффициентов обратной связи размерностью, соответствующей размерности матрицы R; Тs — параметр времени, характеризующий желаемое быстродействие контуров регулирования основной выходной величины. Выбор Тsопределяет полосу пропускания системы и осуществляется исходя из условий ограничения ресурсов управления. В результате при управлении (9) в ориентированной по полю системе координат состояние электрической машины представлено в зависимости от желаемого положения векторов, заданного матрицей В, параметров обратных связей, заданных матрицей К, и сигнала задания Uref выходной величины:

Для выявления элементов матрицы К, определенный выбор которых позволит назвать управление (9) оптимальным, используется принцип максимума Л. С. Понтрягина [3]. На основании этого принципа взаимосвязь между оптимальным управлением, регулируемыми переменными и решениями сопряженной системы устанавливается посредством функции Гамильтона. Поскольку критерием качества является время, рассматривается гамильтониан быстродействия динамической системы (9) в следующем виде:

где составляющие вектора S сопряженной системы:

имеют довольно сложную зависимость во времени:
S(0) — значение вектора сопряженной системы в начальный момент времени.
Из условий стационарности определены требования к управлению [4], отвечающие принципу максимума:
Обязательных требований выполнения условий стационарности является одинаковое изменение во времени составляющих вектора сопряженной системы (12). Так как критерием оптимальности считается время, оптимальное управление должно обеспечивать и наибольшую область устойчивости основной системы [5]. Наибольшей областью устойчивости, а значит, и качеством управления обладают системы, имеющие решения экспоненциального характера. Поэтому желаемые решения сопряженной системы выбраны в следующем виде:

Поскольку в асинхронной короткозамкнутой машине воздействие на канал ротора ограничено, желаемое решение сопряженной системы (11) может быть получено при определенном выборе элементов матрицы К:
V – K = A, (15)
где матрица
характеризует желаемые свойства сопряженной системы. При выполнении условий (15) нетривиальное решение системы уравнений (11):
при равных начальных условиях S(0):
![]()
характеризуется одинаковым изменением во времени проекций вектора сопряженной системы. В силу принятого критерия качества, максимально возможное значение гамильтониана быстродействия равно единице. Это возможно, если при одинаковом изменении составляющих вектора сопряженной системы гамильтониан быстродействия не будет зависеть от задающего воздействия системы управления (1). Выполнение этих условий возможно в том случае, если задание для основной системы уравнений связано с начальными условиями решений сопряженной системы (14):

Основная система уравнений (4) при выполнении условий (15) и формировании управления (9) асинхронной машиной:

имеет решение:
На основании этого решения, при нулевых начальных условиях, получена зависимость электромагнитного момента (5) от его задания:

Подставив решения основной (17) и сопряженной системы (16) в функцию (11), можно убедиться, что аналитические решения являются экстремалями, так как в любой момент времени гамильтониан быстродействия равен единице:

На основании (17) аналитическое решение для регулируемых переменных представлено зависимостью от сигнала задания положительного электромагнитного момента:
Изменение токов во времени определено посредством уравнения (2):
I(t) = L-1Ψ(t). (20)
Решение (17) системы уравнений (1) при формировании управления (9) и выполнении требований (15) отвечает условиям максимума гамильтониана быстродействия, независимо от положения векторов, заданного матрицей В и параметра времени Тs. Определение желаемого энергетического режима работы, обеспечивающего минимизацию реактивной мощности асинхронной машины, осуществляется путем задания параметров вектора управления, выбор которого осуществляется посредством функций энергетического состояния [6]. Условие минимизации реактивной мощности:

достигается при определенном положении вектора потокосцепления статора относительно потокосцепления ротора (8).

Рис. 2. Зависимость потокосцепления ротора от времени при формировании заданного электромагнитного момента
Для асинхронного двигателя 4А100L4 осуществлено численное моделирование процессов формирования электромагнитного момента при экстремальном управлении в условиях cos(j)мах = max. В силу присутствия звена деления в управлении (9), посредством которого обеспечивается линейная зависимость электромагнитного момента от его задания, в модель внесена корректировка, исключающая деление на ноль и обеспечивающая реверсирование выходной величины. На рис. 2, относительно временных интервалов Tr и выбранного значения параметра Ts, представлено изменение во времени электромагнитного момента и потокосцепления ротора при ступенчатом задании электромагнитного момента. На рис. 3 показана реакция системы на изменение знака и величины задания электромагнитного момента.
При нулевых начальных условиях и одинаковом темпе изменения регулируемых величин токи статора и ротора направлены встречно друг другу, что определяет высокое быстродействие управления. Полученные результаты достаточно точно совпадают с выводами, сделанными в работе [7]. Получение желаемого быстродействия контуров, которое характеризуется параметром времени Тs и достигается посредством определенного выбора коэффициентов матрицы обратных связей, зависимость электромагнитного момента от его задания описывается апериодическим звеном первого порядка при оптимальной траектории перехода вектора состояния из одного положения в другое.
Заключение
В рамках единого подхода рассмотрено применение метода синтеза управляющих воздействий, обеспечивающих наиболее быстрое изменение электромагнитного момента асинхронной короткозамкнутой машины в условиях минимизации реактивной мощности. Без предварительного намагничивания магнитной системы показано, что оптимальное управление асинхронной машиной должно осуществляться при одинаковом быстродействии контуров регулируемых переменных. Выбор желаемых энергетических режимов осуществляется путем задания положения вектора регулируемых переменных. Такой подход предоставляет возможность существенно упростить функционал качества и получить аналитические выражения для экстремалей.
- Филюшов Ю. П. Способ оптимального управления электрической машиной // Силовая электроника. 2013. № 2.
- Филюшов Ю. П. Оптимизация электромагнитных процессов в асинхронной короткозамкнутой машине // Электричество. 2011./ № 5.
- Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е.Ф. Математическая теория оптимальных процессов. — М.: Наука, 1976.
- Красовский А. А. Справочник по теории автоматического управления. / Под ред. Красовского А. А. — М.: Наука. Гл. ред. физ. мат. лит., 1987.
- Петров Ю. П. Вариационные методы теории оптимального управления. М. — Л.: Энергия, 1965.
- Филюшов Ю. П. Состояние и оценка качества работы электропривода переменного тока // Силовая электроника. 2013. № 1.
- Филюшов Ю. П. Метод оптимального синтеза управляющих воздействий машины переменного тока // Электротехника. № 8.







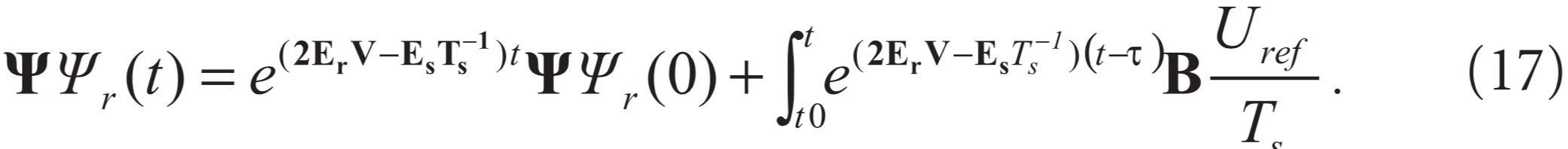


 21 июня, 2016
21 июня, 2016