Реализация защиты преобразователя частоты на основе динамической тепловой модели IGBT силового модуля
Введение
Выбор силовых полупроводниковых приборов, работающих в устройствах с большими кратностями перегрузок по току, в частности в высокодинамичных электроприводах переменного тока с векторным управлением, определяется, как правило, не номинальными значениями нагрузок, а необходимой перегрузочной характеристикой. Эта характеристика определяет зависимость величины тока перегрузки от времени ее действия при заданном температурном режиме работы преобразователя частоты. Важнейшим условием, определяющим надежность преобразователя, является наличие защиты его силовых ключей от теплового разрушения при токовых перегрузках. Наиболее эффективная защита ключей реализуется на основе контроля температуры их кристаллов. Так как непосредственное измерение температуры кристалла произвести весьма проблематично, то защита преобразователя обычно создается на основе контроля температуры в других точках: на охладителе в непосредственной близости от силового модуля, либо с помощью встроенного в модуль датчика, измеряющего температуру корпуса (керамической подложки). Очевидно, что вследствие инерционности датчиков температуры и наличия переходных тепловых сопротивлений «охладитель-корпус» и «корпус-кристалл», контроль температуры в указанных точках может эффективно защищать силовой модуль только при относительно длительных перегрузках с небольшими перегрузками по току. Реализация время-токовой защиты по широко известному критерию 8I 2dt в случае с кратковременными перегрузками IGBT также не способна защитить кристалл от теплового разрушения. В результате приходится ограничивать допустимую величину перегрузки по току на заведомо заниженном уровне, чтобы кратковременные пики тока, не отслеживаемые датчиком температуры, не приводили к тепловому разрушению кристалла, либо выбирать силовые модули с неоправданно большим запасом. Существенно расширить диапазон допустимых токовых перегрузок (в некоторых режимах работы электропривода более чем на 50%) позволяет построение температурной защиты преобразователя частоты на основе динамической модели тепловых процессов IGBT силового модуля.
Методология и алгоритмы расчета потерь в элементах силового модуля и температуры кристаллов достаточно хорошо изложены в публикациях ведущих производителей IGBT, таких как EUPEC, Semikron, Mitsubishi, и в других работах [1-3]. В настоящее время ведущие фирмы распространяют на своих сайтах программы для автоматического теплового расчета и выбора IGBT силовых модулей — IPOSIM, SEMISEL, MelcoSim [4]. Эти программы и положенные в их основу алгоритмы расчетов специально разрабатывались для автоматизации анализа теплового состояния силовых ключей и процесса выбора модуля на этапе проектирования изделия по наиболее напряженному квазиустановившемуся тепловому режиму. Программы оснащены хорошими средствами визуализации входных данных и результатов расчета. Результаты тепловых расчетов представляются в виде набора функциональных зависимостей потерь, температур, предельных выходных токов IGBT-модуля от режима его работы. В качестве исходных данных задаются тип силового модуля и его корпуса, а также интегральные характеристики выбранного установившегося режима работы: действующее значение выходного тока; диапазон частот основной гармоники выходного напряжения; частота ШИМ; входное напряжение инвертора; коэффициент модуляции; cos(φ) нагрузки; температура корпуса. Если в тепловой расчет входит выбор системы охлаждения, как у фирмы Semikron, то дополнительно задаются необходимые для этого параметры, а именно: температура окружающей среды; количество ключей параллельно соединенных модулей на одном радиаторе; способ охлаждения; скорость воздуха или жидкости в системе принудительного охлаждения; тепловое сопротивление «теплосток — окружающая среда».
Однако принятый в этих моделях алгоритм вычислений, основанный на задании интегральных параметров установившегося режима работы, и, тем более, форма представления результатов, получаемых в процессе расчетов, не удобны для построения температурной защиты IGBT-модуля по следующим причинам:
- Эффективная тепловая защита должна в реальном масштабе времени учитывать изменения всех основных параметров, влияющих на мгновенное значение температуры кристалла, во всех возможных режимах работы электропривода — как в статических, так и в динамических.
- В реальном частотно-регулируемом электроприводе частота основной гармоники, выходной ток, коэффициент модуляции, cos(cp) являются переменными величинами, изменяющимися в широких пределах.
- Частота модуляции в современных электроприводах также является переменной. В системах с жестким законом формирования ШИМ [5] она доступна для изменения пользователю в широких пределах (от единиц до десятков килогерц). В системах с релейным способом формирования ШИМ, в частности, в системах прямого управления моментом и в системах с релейным контуром тока [6], понятие фиксированной частоты модуляции вообще отсутствует.
- Тепловая защита должна учитывать особенности конкретного алгоритма формирования ШИМ и ограничения, связанные с «неидеальностями» динамических свойств силовых ключей [5] и системы управления.
Тепловая модель IGBT силового модуля
Базовые принципы и допущения, принятые при построении тепловой модели
1) Тепловой расчет выполняется на основе информации о мгновенных значениях переменных: токов, протекающих через элементы силового модуля (транзисторы и обратные диоды); входного напряжения инвертора; мгновенного состояния всех элементов модуля. Такой подход обеспечивает инвариантность алгоритма теплового расчета к интегральным, усредненным на периоде основной гармоники, значениям переменных, а также к способу формирования и виду ШИМ. Усреднение переменных допускается только на малых интервалах, значения которых меньше самой малой тепловой постоянной времени кристаллов. Анализ параметров тепловых моделей силовых модулей серий FP, FS с IGBT 3-го поколения фирмы EUPEC показал, что тепловые постоянные времени кристаллов в основном лежат в интервале 0,002-0,1 °C. Среднеквадратичная оценка постоянной времени кристаллов при аппроксимации тепловой модели одним экспоненциальным участком составляет величину, близкую к 0,03 °C для всех типоразмеров модулей. С учетом этого интервал усреднения потерь может выбираться из условия: Thc ≤ 2 мс. Полагаем, что на интервалах времени, меньших Thc, надежную защиту силового модуля обеспечивает двухуровневая максимально-токовая защита: первый уровень — программный (на основе измерения мгновенных значений выходных токов фаз), второй — аппаратный, реализованный на основе контроля насыщения IGBT.
2) Наиболее эффективная защита от теплового разрушения кристаллов во всех возможных режимах работы инвертора, в том числе и при несимметричной загрузке силовых ключей, реализуется на основе поэлементного расчета температуры всех транзисторов и обратных диодов IGBT-модуля. Уменьшить количество участвующих в тепловом расчете элементов силового модуля можно, вводя дополнительные ограничения на допустимые режимы работы преобразователя, например:
- ограничение величины тока в генераторных режимах работы нагрузки преобразователя (cos(φ) на определенном расчетном уровне позволяет контролировать температуру только транзисторов модуля, так как температура обратных диодов оказывается заведомо ниже предельно допустимых значений;
- допущение о симметрии выходных токов преобразователя позволяет строить его тепловую защиту на основе контроля температур элементов одного плеча трехфазного моста.
3) Временные изменения температуры, вызванные взаимосвязью отдельных элементов силового модуля, пренебрежимо малы по сравнению с эффектами самонагрева кристаллов [1]. Увеличение температуры из-за тепловой связи элементов друг с другом может считаться относительно медленно изменяющейся величиной, измеряемой встроенным датчиком температуры корпуса IGBT силового модуля.
4) Потери включения диода пренебрежимо малы по сравнению с потерями выключения.
Основные этапы расчета тепловых процессов IGBT-модуля, выполняемые на каждом интервале усреднения потерь:
- расчет времени проводящего состояния элементов силового модуля: Tcondi, где I = 1, 2…p, p — число элементов модуля, участвующих в его тепловом расчете;
- расчет числа включений (Non) и выключений (Noffr) элементов силового модуля;
- расчет тока через элемент (I );
- расчет мощности потерь в элементах инвертора;
- расчет температуры кристаллов.
Рассмотрим этапы расчета тепловых процессов модуля более подробно. Топология цепей силового модуля и нагрузки с принятыми обозначениями, нумерацией элементов и датчиками представлены на рис. 1.

Рис. 1. Топология цепей IGBT силового модуля и нагрузки
Расчет времени проводящего состояния и числа переключений выполняется на основе определения состояния элемента (проводит или не проводит ток) в каждый текущий момент времени. Текущее состояние каждого элемента силового модуля однозначно характеризуется мгновенными значениями выходных напряжений и направлениями выходных токов ПЧ. Однако измерять все эти шесть переменных нецелесообразно. В типовой набор переменных, измеряемых в электроприводе с преобразователем частоты, входит два выходных фазных тока Ia, Ib, входное напряжение инвертора Ud и температура корпуса модуля Θcase. В качестве информации о выходном напряжении удобно использовать логические сигналы управления фазами инвертора, образующие вектор управляющих воздействий Uy (Sua, Sub, Suc), учитывая при этом измеряемое значение Ud. Логической единице соответствует подключение фазы нагрузки к положительному, а логическому нулю — к отрицательному полюсу источника питания инвертора. Направления выходных токов инвертора определим трехкомпонентным вектором логических сигналов SI (SIa, Sib, SIc). Логической единице соответствует направление тока от инвертора к нагрузке, логическому нулю — от нагрузки к инвертору.
Чтобы указанный набор измеряемых и формируемых в процессе управления переменных был достаточным для оценки мгновенного состояния элементов инвертора, необходимо принять следующие допущения:
- в выходных токах отсутствует нулевая последовательность фаз, то есть выполняется условие Ic = -(Ia+Ib);
- транзисторы, относящиеся к одной фазе моста, коммутируются в противофазе, то есть состояние шести транзисторов инвертора однозначно характеризуется тремя логическими сигналами состояния фаз (Sua, Sub, Suc).
Введем понятие вектора проводящих элементов Cnd (Cnda, Cndb, Cndc), составленного из порядковых номеров элементов инвертора, проводящих выходные фазные токи, при заданном состоянии управляющих воздействий и выходных токов.
В таблице 1 приведены компоненты вектора проводящих элементов при всех возможных сочетаниях управляющих воздействий и токов.

Время проводящего состояния каждого элемента Tcondi на интервале усреднения потерь Thc рассчитывается как сумма всех времен проводящих состояний элемента на данном интервале. Анализ нового состояния элементов выполняется при каждом изменении вектора управляющих воздействий U и вектора направления выходных токов SI. В системах с жестким законом формирования ШИМ по «треугольному» алгоритму [5] оценку вектора направления токов допускается выполнять один раз за период модуляции посередине интервала включения нулевого вектора.
Расчет числа включений и выключений элементов силового модуля выполняется на основе анализа изменений в каждом новом векторе проводящих элементов относительно его предыдущего состояния и поэлементного суммирования всех включений и выключений на интервале усреднения потерь. В системах с жестким законом формирования ШИМ учет новых переключений допускается выполнять один раз на периоде модуляции. В системах с релейным способом формирования ШИМ учет новых переключений выполняется при каждом изменении вектора управляющих воздействий.
Расчет токов, протекающих через элементы инвертора на интервале усреднения потерь, выполняется на основе информации о мгновенных значениях выходных токов по следующему алгоритму:
- вычисляется мгновенное значение тока элемента. Соответствие между мгновенными токами, протекающими через проводящий элемент, и выходными токами инвертора устанавливается по таблице 2.
- ток элемента на интервале усреднения потерь вычисляется по формуле:
где Ii— ток элемента на i-м участке проводимости; τi— продолжительность участка проводимости; k— общее число участков проводимости элемента на интервале усреднения потерь.

В системах с жестким законом формирования ШИМ по «треугольному» алгоритму допускается применение упрощенного способа расчета среднего тока элемента по формуле:
где Ii — эквивалентный (усредненный на периоде модуляции) ток элемента, вычисленный по замеру мгновенного выходного тока инвертора в середине интервала включения нулевого вектора напряжения; n — число периодов модуляции на интервале усреднения потерь.
Расчет мощности потерь в элементах инвертора
Потери проводимости (статические потери):
 (1)
(1)где Uν(Iν)— зависимость падения напряжения на элементе от его тока. Для IGBT — это зависимость напряжения «коллектор — эмиттер» от тока коллектора при нормированных значениях напряжения «затвор — эмиттер» и температуры кристалла. Для обратного диода — это зависимость его прямого напряжения от тока при нормированном значении температуры кристалла. Зависимости Uν(Iν) предоставляются фирмой-производителем модулей и с достаточной степенью точности описываются с помощью линейной аппроксимации:
Uν = Uν0 + RνIν
Где Uν0, Rν — параметры линейной аппроксимации.
Потери переключения (динамические потери) элемента вычисляются по формуле:
 (2)
(2)где Non, Noff— число включений и отключений элемента на интервале усреднения потерь; Won(Iν), Woff(Iν) — зависимости энергий включения и выключения элемента от его тока. Зависимости предоставляются фирмой-производителем при нормированных значениях входного напряжения инвертора, температуры кристалла, напряжения «затвор — эмиттер» и сопротивлений, входящих в цепь затвора при включении и отключении транзистора. Для обратного диода энергия перехода в открытое состояние пренебрежимо мала в сравнении с энергией обратного восстановления и в расчетах не учитывается.
В пределах ограниченной области изменения фактического значения входного напряжения Ud относительно его нормированного значения Ud nom (приблизительно ±20%) допускается линейная аппроксимация зависимости потерь переключения от входного напряжения инвертора [2].
Аналитическое задание функциональных зависимостей энергий включения и выключения с необходимой степенью точности осуществляется с помощью кусочно-линейной аппроксимации. Как правило, достаточно двух линейных участков.
В последнее время при уточненных расчетах тепловых режимов IGBT силовых модулей стали учитывать потери на активном сопротивлении выводов. Это связано с тем, что зависимостиUν(Iν) элементов силового модуля обычно определяются относительно его выходных выводов, и часть потерь проводимости, происходящих непосредственно на выводах модуля, нужно рассматривать как внешние, не участвующие в нагреве кристалла. Расчет потерь на выводах модуля выполняется по формуле:

где Rt— активное сопротивление выводов силового модуля, рассчитанное для рабочего значения их температуры. Рабочая температура выводов принимается равной температуре корпуса. В справочных данных приводится сопротивление выводов модуля при нормированном значении температуры.
Полные потери элемента IGBT силового модуля, идущие на нагрев кристалла, определяются на интервале усреднения потерь как сумма потерь проводимости и потерь переключения за вычетом потерь на выводах:
Pν = Ps + Pd – Pt . (3)
Расчет температуры кристаллов
Тепловая структура стандартного IGBT силового модуля является восьмислойной, состоящей из следующих слоев [1]: 1 — вывод кристалла (Al), 2 — кристалл (Si), 3 — припой, 4 — металлизация (Cu), 5 — керамическая подложка (Al2O3), 6 — металлизация (Cu), 7 — припой, 8 — основание модуля (Cu). Каждый слой обладает своей геометрией, теплоемкостью и теплопроводностью, которые сильно варьируются от одного слоя к другому. Процесс нагрева однородного слоя описывается экспоненциальной зависимостью температуры перегрева от мощности потерь. В связи с этим, переходное тепловое сопротивление многослойной структуры IGBT-модуля принято описывать в виде суммы экспоненциальных зависимостей ее отдельных участков:
 (4)
(4)где I = 1, 2… п, п — количество участков разбиения рассматриваемой области IGBT силового модуля; Rν,i, τν,i — тепловое сопротивление и эквивалентная постоянная времени нагрева г’-го участка.
В общем случае все эти участки являются воображаемыми, их количество и параметры не соответствуют числу и параметрам реальных слоев в структуре силового модуля. Выбор количества участков определяется желаемой точностью воспроизведения переходного теплового сопротивления IGBT.
Встроенный датчик температуры IGBT силовых модулей 3-го поколения фирмы EUPEC устанавливается на керамической подложке, являющейся корпусом для транзисторов и диодов модуля. Считаем, что датчик, установленный, как правило, в центре основания силового модуля, измеряет среднюю температуру корпуса Θcase Постоянная времени датчика составляет величину порядка 2 с. Она много больше тепловой постоянной времени кристалла и много меньше эквивалентной постоянной времени всей системы охлаждения, включающей, помимо модуля, радиатор и отвод тепла от радиатора в окружающую среду. Таким образом, датчик способен адекватно отслеживать тепловое состояние модуля только при относительно длительных токовых перегрузках. Данные его измерений могут быть использованы в качестве точки отсчета при расчете температуры кристалла на основе информации о переходном тепловом сопротивлении области «корпус-кристалл» IGBT силового модуля.
Температура кристалла в конце интервала усреднения потерь рассчитывается по выражению:
 (5)
(5)где
 ΔΘm,i = Rν,i Pν — установившееся значение перегрева г’-го участка; ΔΘm,i, ΔΘiν(0)— мгновенные значения температуры перегрева г’-го участка в конце и в начале интервала усреднения потерь.
ΔΘm,i = Rν,i Pν — установившееся значение перегрева г’-го участка; ΔΘm,i, ΔΘiν(0)— мгновенные значения температуры перегрева г’-го участка в конце и в начале интервала усреднения потерь.Тепловую модель кристалла IGBT силового модуля можно представить в виде эквивалентной электрической схемы замещения (рис. 2). Потери в кристалле представляются в виде источника тока, превышения температур на отдельных участках — в виде падений напряжения на параллельно включенном активном сопротивлении и емкости участка, температура корпуса вводится в модель в виде источника ЭДС. Постоянная времени нагрева г’-го участка определяется выражением: τν,i = Rν,iCν,i.

Рис. 2. Эквивалентная электрическая схема замещения тепловой модели кристалла
С целью определения оптимального количества участков, на которые разбиваются области «корпус-кристалл» при построении динамической модели тепловых процессов IGBT силового модуля, выполним анализ точности аппроксимации переходного теплового сопротивления согласно (4) при различном числе участков (n= 1, 2, … 5). Определение коэффициентов функции, аппроксимирующей переходное тепловое сопротивление, произведем на основе минимизации среднеквадратического отклонения по критерию:
при наложении следующих ограничений:
Rν,I > 0; τν,i> 0,
где Zνr(tj), j = 1…k — таблично заданная в k дискретных точках зависимость переходного теплового сопротивления «корпус-кристалл», предоставляемая фирмой-производителем IGBT-модулей. Условие разрешимости задачи: k ≥ 2n.
Данная задача была решена средствами программной среды Mathcad. В частности, для модуля FP25R12KE3 фирмы EUPEC получены результаты, представленные в таблицах 3, 4.


Из приведенных результатов видно, что увеличение количества участков с одного до двух и с двух до трех позволяет уменьшить предельное относительное отклонение приблизительно в 7 и 13 раз соответственно. Дальнейшее увеличение количества участков приводит к существенно меньшему повышению точности аппроксимации переходного теплового сопротивления.
Увеличение количества участков выше 4 практически нецелесообразно по критерию «точность аппроксимации». Следует помнить, что точность аппроксимации должна соответствовать точности технической информации о тепловых характеристиках модуля, предоставляемой фирмой-производителем. Как правило, задание переходного теплового сопротивления с точностью 3-5% является вполне достаточной. Кроме точности вычислений, при выборе тепловой модели, работающей в реальном масштабе времени, следует учитывать критерий временных затрат на вычисления. При учете всех указанных факторов для расчета мгновенного значения температуры элементов IGBT-модуля можно рекомендовать динамические модели, построенные по уравнениям (1-5), с двумя и тремя участками разбиения области «корпус-кристалл».
Эффект увеличения перегрузочной способности преобразователя с защитой по динамической тепловой модели IGBT силового модуля
Условие срабатывания защиты от токовых перегрузок, построенной по динамической тепловой модели IGBT-модуля, определим как превышение температурой любого из кристаллов модуля порога предельно допустимой рабочей температуры кристалла:
max (Θν,i )i = 1…p > Θν_max).
Величина Θν_max устанавливается исходя из требований фирмы-производителя IGBT силовых модулей, с учетом предельных значений для ошибок вычисления температуры кристалла. Типовое значение для преобразователей частоты серии ЭПВ [7]: 125 °С.
Традиционный способ тепловой защиты преобразователя основан на контроле температуры датчика, измеряющего температуру радиатора, или встроенного датчика, измеряющего температуру подложки силового модуля. Вследствие того, что тепловые постоянные времени кристаллов на несколько порядков меньше постоянных времени датчиков температуры радиатора и подложки модуля, контроль этих температур сам по себе не способен надежно защитить силовой модуль от больших кратковременных токовых перегрузок. Важнейшим фактором построения тепловой защиты в этом случае становится ограничение предельного значения тока перегрузки. Если этот ток рассчитать исходя из тепловых процессов модуля, то он оказывается сложной функцией многих переменных, среди которых время перегрузки, частота основной гармоники (f), частота ШИМ (fмод), входное напряжение инвертора, коэффициент модуляции (Kмод), cos(φ) нагрузки, температура корпуса элементов модуля. Так как задать данную функцию в реальном времени работы преобразователя весьма проблематично, то обычно поступают следующим образом: предельно допустимое значение выходного тока Imax принимают постоянным, исходя из выбранного типового режима работы преобразователя. Выбор типового режима для расчета Imax является прерогативой разработчика. В качестве примера в таблице 5 приведены предельные значения выходного тока для различных режимов работы модуля FP50R12KE3 фирмы EUPEC, рассчитанные с помощью программы IPOSIM6.0a.

Заметим, что паспортное значение предельно допустимого постоянного тока модуля, заявленное фирмой-производителем при Tcase = 80 °C, составляет 50 А, а повторяющийся пиковый ток с длительностью импульса 1 мс и Tcase = 80 °C — 100 А.
Режим 1 рассмотрим как базовый. Режимы 2-8 показывают, как изменяется Imax при вариации одного из параметров режима работы относительно параметров базового режима. Режим 9 представляет собой наихудшую комбинацию параметров режима работы преобразователя в рассматриваемых диапазонах их вероятных изменений.
Таким образом, при традиционном способе построения тепловой защиты пиковый выходной ток преобразователя вне зависимости от продолжительности его протекания не должен превышать значения Imax, определенного из тепловых условий продолжительного режима работы. Для надежной тепловой защиты преобразователя с указанными в таблице 5 диапазонами изменения параметров режима работы следует принимать Imax = 23 A. Очевидно, что при других сочетаниях параметров режима модуль оказывается существенно недоиспользованным.
Построение защиты преобразователя на основе динамической тепловой модели IGBT силового модуля позволяет значительно повысить порог ограничения выходного тока. Он может быть установлен на уровне повторяющегося пикового тока с длительностью импульса tимп ≥ Thc Если принять интервал усреднения тепловых потерь (период расчета тепловых процессов) Thc = 1 мс, то для модуля FP50R12KE3 получим Imax = 100 A при Tcase = 80 °C, то есть в 4,3 раза выше, чем ограничение тока при традиционном способе построения тепловой защиты. Допустимая продолжительность работы преобразователя с заданным уровнем тока автоматически определяется в динамической тепловой модели в зависимости от текущих мгновенных значений параметров режима работы. Таким образом, прямым следствием введения тепловой защиты по динамической тепловой модели IGBT-модуля является значительное повышение перегрузочной способности преобразователя в режимах кратковременных перегрузок (от 0,001 до 10 с).
Экспериментальные результаты
С целью анализа квазиустановившихся и динамических тепловых процессов, протекающих в элементах IGBT силового модуля при его работе в составе частотно-регулируемого электропривода, было проведено математическое моделирование асинхронного электропривода с преобразователем частоты, оснащенным представленной выше тепловой моделью. Моделирование выполнено в среде Delphi. На рис. 3-6 изображены временные диаграммы тепловых процессов, полученные в различных режимах работы преобразователя частоты с IGBT-модулем FP50R12KE3 фирмы EUPEC, который нагружен асинхронным двигателем 4А180М4У3, при следующих условиях: закон модуляции напряжения — синусоидальный; Ud = 520 В; fмод = 4000 Гц; способ управления электроприводом — адаптивно-векторный [5]. Все процессы показаны без учета эффекта срабатывания тепловой защиты.
На рис. 3 приведены временные диаграммы фазных токов, усредненных на интервале модуляции, потерь Pν,1, Pν,2, Pν,3,и температур кристаллов Θν,1, Θν,2, Θν,3 транзисторов V1, V2, V3 верхнего плеча инвертора. Диаграммы получены в установившемся режиме работы преобразователя частоты при следующих условиях: действующее значение тока фазы Iпч = 44,7 А; f= 10 Гц; Кмод = 0,23; cos(φ) = 0,91; Tcase = 68 °C;

Рис. 3. Временные диаграммы фазных токов, потерь и температур кристаллов IGBT в установившемся режиме при синусоидальном законе модуляции
На рис. 4 приведены временные диаграммы скорости двигателя, тока фазы А, потерь и температуры кристалла транзистора V1 в переходном режиме разгона двигателя с ω=20 рад/с до ω = 120 рад/с с моментом нагрузки Mc = 0,5Mnom и Tcase = 40 °C.
На рис. 5 приведены временные диаграммы скорости двигателя, действующего значения выходного тока преобразователя, температур кристаллов всех шести транзисторов V1…V6 IGBT-модуля в режиме разгона двигателя с ω=20 рад/с до ω= 100 рад/с при Tcase = 64 °C.

Рис. 5. Динамические процессы в режиме разгона двигателя с ω = 20 рад/с до ω = 100 рад/с с моментом нагрузки Мс = 0,5 Мnom, Tcase = 64 °C
На рис. 6 приведены временные диаграммы скорости двигателя, активной составляющей выходного тока преобразователя Iакт, максимальных значений температур транзисторов (Θmax_t) и обратных диодов (Θmax_d), полученные в режиме реверса скорости двигателя с ω= 100 рад/с при Tcase = 40 °C. Максимальные значения температур транзисторов и обратных диодов определяются выражениями:
где i — порядковый номер элемента модуля согласно рис. 1.

Рис. 6. Динамические процессы в режиме реверса скорости ненагруженного двигателя с ω = 100 рад/с, Tcase = 40 °C
Из диаграмм видно, что в установившихся режимах работы при симметричной загрузке фаз процессы изменения температуры всех биполярных транзисторов IGBT силового модуля идентичны по форме и сдвинуты друг относительно друга на углы, кратные π/3. В переходных режимах форма процессов и предельные значения температур кристаллов могут существенно отличаться друг от друга.
Следовательно, для построения надежной тепловой защиты в динамических режимах требуется информация о температурах всех элементов силового модуля. Точная оценка температур одних элементов модуля на основе информации о температурах других его элементов не представляется возможной, так как соотношения между ними существенно нелинейны даже при наличии симметрии фазных токов.
Из графиков на рис. 4-5 видно, что кратковременная работа с токами, близкими к удвоенному значению предельно допустимого постоянного тока модуля вполне возможна по температурным условиям. Однако в реальном электроприводе она может осуществляться только при наличии эффективной тепловой защиты, построенной по динамической тепловой модели IGBT-модуля. Момент срабатывания тепловой защиты (tср) определяется первым пересечением кривой температуры наиболее нагретого элемента модуля (Θν,1 на рис. 5) с заданным порогом срабатывания защиты Θy,
Из рис. 6 видно, что в режиме рекуперации энергии при торможении (I акт < 0) максимальные значения температур обратных диодов превышают максимальные значения температур транзисторов, а в режиме потребления энергии при разгоне (Iакт > 0) — все наоборот. Таким образом, если преобразователь должен обеспечивать большие кратности токовых перегрузок в режимах рекуперации энергии, то встроенная тепловая модель силового модуля должна включать в себя расчет температур кристаллов обратных диодов.
Реализация и промышленное внедрение
Реализация рассмотренного способа защиты была выполнена путем разработки специальных подпрограмм для микроконтроллера ADMC-401, являющегося ядром системы управления преобразователей серии ЭПВ. Полный алгоритм расчета разбит на два цикла — быстрый (равный периоду ШИМ), в течение которого выполняется расчет количества переключений и длительности интервалов проводимости каждого ключа, и медленный (1 мс), в котором выполняется вычисление статических и динамических потерь и величины перегрева каждого из кристаллов относительно температуры корпуса. При перегрузках, длящихся менее 1 мс, действует алгоритм защиты по максимальному току.
Отладка программного обеспечения и проверка результатов моделирования выполнялась на экспериментальной установке (рис. 7), состоящей из механически связанных асинхронного и синхронного двигателей, подключенных к прототипам преобразователей частоты. Каждый из двигателей может быть как испытуемым, так и нагрузочным, работая в двигательном или генераторном режиме соответственно. Благодаря использованию рекуперативного выпрямителя обеспечена возможность создания нагрузки в длительном режиме на любом уровне скорости. Датчиковая система позволяет регистрировать все необходимые для проверки переменные:
- выпрямленное напряжение;
- токи фаз двигателей;
- скорость двигателя;
- частоту выходного напряжения преобразователя частоты;
- действующее значение выходного напряжения преобразователя частоты;
- измеренную температуру радиатора преобразователя частоты;
- вычисленные температуры IGBT-кристаллов преобразователя частоты.

Рис. 7. Общий вид экспериментальной установки
В качестве критериев проверки было принято соответствие результатов расчета мгновенных значений для температуры кристаллов IGBT, полученных с помощью программы IPOSIM-6.0 и выдаваемых моделью, встроенной в преобразователь, а также отсутствие отказов в предельных режимах работы.
Соответствие проверялось в типовых режимах работы при вариации параметров этих режимов: выходного тока преобразователя, частоты основной гармоники, частоты модуляции. Проверка показала, что во всех типовых режимах отклонение предельных значений температур не превышает ±4 °С. Максимальная величина этих отклонений наряду с максимальной погрешностью датчика температуры корпуса учтена при выборе порога срабатывания тепловой защиты.
Проверка функционирования защиты в предельных режимах проводилась сначала при пониженном пороге срабатывания с постепенным повышением его до расчетного максимума. На рис. 8 приведены осциллограммы мгновенных значений тока выходной фазы и температуры одного из кристалла IGBT в процессе пуска электропривода под нагрузкой. Перед проверкой выполнялся прогрев преобразователя, нагруженного на асинхронный двигатель в длительном режиме до установившейся температуры корпуса IGBT силового модуля. Виден момент срабатывания защиты с мгновенным прерыванием тока при достижении порога 126 °С и последующее снижение температуры кристалла. Преобразователь был оснащен модулем типа FP50R12KE3 (EUPEC) с максимально допустимым длительным током 50 А при температуре корпуса 80 °С. Процесс пуска до срабатывания защиты длился 90 мс, пиковые значения тока при этом достигали 81 А.

Рис. 8. Осциллограммы температуры кристалла IGBT и тока фазы V инвертора при срабатывании защиты в процессе пуска двигателя под нагрузкой. QVmax = 126 °C, IVmax = 81 А
После отладки программного обеспечения и проверки функционирования защита была внедрена во всех типоразмерах преобразователей частоты серии ЭПВ, выпускаемых ООО «ЭЛПРИ» Чебоксарского электроаппаратного завода. Проверка защиты проводилась для каждого типоисполнения преобразователя по мощности. Отказов в процессе проверки не было.
Заключение
- Предложена методика расчета температуры кристаллов IGBT силового модуля, работающего в составе преобразователя частоты, основанная на информации о мгновенных значениях выходных токов, входного напряжения и вектора управляющих воздействий инвертора, а также на технической информации о параметрах модуля, предоставляемой фирмой-производителем.
- В рамках предложенной методики разработана тепловая модель IGBT-модуля, позволяющая производить вычисления мгновенных значений температуры всех его кристаллов, в том числе в реальном времени функционирования преобразователя. Назначение модели: анализ теплового состояния IGBT силового модуля в квазиустановившихся и переходных режимах работы электроприводов с преобразователями частоты; построение надежной тепловой защиты преобразователя при его работе в режиме кратковременных перегрузок с большими кратностями токов.
- Применение тепловой защиты преобразователя, построенной на основе динамической тепловой модели IGBT силового модуля, обеспечивает повышение перегрузочной способности преобразователя за счет увеличения предельно допустимого выходного тока вплоть до уровня повторяющегося пикового тока модуля с длительностью импульса, равного интервалу усреднения потерь тепловой модели.
- Достоверность результатов, полученных с помощью предложенной модели, подтверждена сравнением с результатами расчетов, выполненных на модели IPOSIM6, рекомендуемой фирмой EUPEC для расчета температурных режимов модулей своего производства.
- Для реализации защиты разработано программное обеспечение для микроконтроллера ADMC-401. Проверка функционирования подтвердила результаты модельного эксперимента.
- Промышленное внедрение результатов работы осуществлено в преобразователях частоты серии ЭПВ, выпускаемых ООО «ЭЛПРИ» Чебоксарского электроаппаратного завода [8].
- Sven Konrad. Тепловые параметры силовых модулей в широтно-импульсных преобразователях. В кн. Силовые IGBT-модули. Материалы по применению. М.: ДОДЭКА. 1997.
- Dimensioning program IPOSIM for loss and thermal calculation of eupec IGBT modules. Technical documentation.
- Колпаков А. Особенности теплового расчета импульсных силовых каскадов // Компоненты и технологии. 2002. № 1.
- Колпаков А. MELCOSIM? IPOSIM? SEMISEL? О выборе и замене модулей IGBT // Силовая электроника. 2005. № 1.
- Виноградов А. Б., Чистосердов В. Л., Сибирцев А. Н. Адаптивная система векторного управления асинхронным электроприводом // Электротехника. 2003. № 7.
- Виноградов А. Б. Цифровая релейно-векторная система управления асинхронным электроприводом с улучшенными динамическими характеристиками // Электричество. 2003. № 6.
- Виноградов А. Б., Сибирцев А. Н., Чистосердов В. Л. Новые серии преобразователей частоты и объектно-ориентированный электропривод на их основе // Электротехника. 2005. № 5.
- Степанов В., Матисон В., Виноградов А., Сибирцев А., Лавров А., Бахарев П., Прокудин А. Новые средства энергосбережения и оптимизации энергопотребления // Силовая электроника. 2005. № 3.



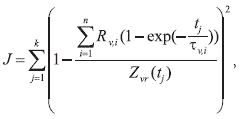
 2 мая, 2012
2 мая, 2012 6 августа, 2020
6 августа, 2020