Способ оптимального управления электрической машиной
Можно выделить ряд фирм, занимающих лидирующее место в производстве электропривода переменного тока. По аналогии с управлением машиной постоянного тока, существующие законы определены концепцией управления при постоянном значении энергии магнитного поля, частным случаем которой является управление при стабилизации потокосцепления. Это направление было сформулировано Феликсом Блашке (Felix Blaschke) в 1971 г. и до настоящего времени считается доминирующим при формировании электромагнитного момента в системе векторного управления машиной переменного тока [1]. Несмотря на широкое применение, формирование электромагнитного момента в условиях стабилизации потокосцепления статора или ротора имеет ряд существенных недостатков. К ним относится значительное ухудшение энергетической эффективности работы электрической машины при отклонении нагрузки от номинальной величины. Ясно видна ограниченность ресурсов по управлению и сложность достижения больших скоростей движения.
Осуществляя предварительное намагничивание магнитной системы, электрическая машина, представлена в виде одноканальной системы, для которой довольно легко подобрать соответствующий метод синтеза. Введение в управление разомкнутых компенсационных каналов и дифференциальных связей, синтезированных из того или иного условия инвариантности ошибки относительно задающего или возмущающего воздействия, предполагает расширение возможности улучшения качества динамических процессов. Но эффект влияния принимаемых решений на показатели качества системы управления зависит от уровня ограничения сигналов нелинейными элементами. Выходные сигналы, обычно кратковременные по длительности и значительные по амплитуде, ограничиваются и не приводят к желаемому улучшению качества работы электропривода [2].
Для многоканального объекта управления, каким является машина переменного тока, выбор метода синтеза управляющих воздействий всегда является проблемой.
Сложность выбора объясняется тем, что величина электромагнитного момента электрической машины зависит от произведения регулируемых переменных, способных изменяться во времени различным образом. Многообразие траекторий регулируемых переменных ставит задачу выбора наилучшей траектории и существенно усложняет задачу формирования заданной величины электромагнитного момента, при стандартном характере переходных процессов. Являясь энергосиловой установкой, электропривод, кроме динамических показателей качества, должен наилучшим образом отвечать и энергетическим требованиям, предъявляемым к современному технологическому оборудованию.
Исследование процессов электромеханического преобразования энергии показывает, что энергетические и динамические свойства работы электрической машины зависят от траектории движения и конечного положения вектора регулируемых переменных. Поэтому в качестве выходных величин, помимо электромагнитного момента, могут выступать такие энергетические характеристики, как коэффициент полезного действия или cosφ, характеризующий использование электромагнитной мощности двигателя. Выбор траектории регулируемых переменных по тому или иному критерию качества является задачей поиска наилучшего управления. Известные методы оптимального управления, в силу сложности математического описания машины переменного тока и неоднозначности формальной части задачи управления, не нашли своего широкого применения. Трудности выбора критерия оптимальности объясняются тем, что требования, предъявляемые к работе электропривода, противоречивы, а сложность решения задачи управления зависит от сложности функционала. Если функционал отвечает большому количеству требований к работе электропривода, то аналитический синтез управляющих воздействий практически невозможен. Поэтому наилучшее управление в явном виде следует искать при наиболее полном использовании физических свойств электрической машины, применяя наиболее простые функционалы [3]. Если рассматривать в качестве функционала T время
то решение оптимальной задачи управления одновременно позволит решить задачу наибольшей области устойчивости системы, а следовательно, и качества управления [4]. Посредством применения функций энергетического состояния и принципа максимума [5] разработан метод синтеза, позволяющий формировать управление, обеспечивающее наилучшее сочетание динамических и энергетических свойств работы электрической машины.
В работе ставится задача определения вектора воздействий, принадлежащего замкнутой области пространства допустимых управлений, обеспечивающего в условиях заданных энергетических требований перевод системы (1) из начального состояния в состояние, определенное заданной величиной электромагнитного момента за минимальное время. Под допустимым управлением из всех возможных понимается управление, позволяющее сформировать предписанное значение электромагнитного момента, величина которого зависит от произведения регулируемых переменных, способных изменяться по любой из множества траекторий.
Поскольку заданные энергетические требования существенно сужают область допустимых управлений, их можно рассматривать как энергетические ограничения, в качестве которых могут выступать режимы работы, не обеспечивающие изменение электромагнитного момента в условиях минимума мощности или напряжения, подводимого к обмоткам двигателя, максимума cos(φ) или минимума мощности тепловых потерь. Решение поставленной задачи основано на анализе электромагнитных процессов формирования электромагнитного момента. Учитывая многообразие объектов управления, в качестве электромеханического преобразователя энергии исследуется обобщенная электрическая машина. Математическое описание представлено уравнениями Кирхгофа, описывающими состояние электрической машины в системе вращающихся со скоростью ротора ω координат d, q:
где: ud, uq, urd, urq — напряжения статора и ротора, подводимые к обмоткам двигателя; id, iq, ird, irq, Ψd, Ψq, Ψrd, Ψrq — соответствующие токи и потокосцепления статора и ротора в системе рассматриваемых координат; Rs, Rr — активные сопротивления обмоток статора и ротора. Взаимосвязь токов и потокосцеплений определена в векторной форме посредством следующих уравнений:
где
L-матрицы индуктивностей и активных сопротивлений R, матрицы токов I и потокосцеплений Ψ; Ω — матрица величин, характеризующих скорость вращения ротора; Ls, Lr — индуктивности обмоток статора и ротора; Lm — взаимная индуктивность статора и ротора. В качестве регулируемых переменных динамической системы (1) выбраны потокосцепления. Такое решение позволит наиболее просто учесть нелинейность характеристики намагничивания реальной машины. Полагая, что путем измерения токов, напряжений и угловой частоты вращения ротора вектор регулируемых переменных Ψ вычисляется достаточно точно, примем условие полной наблюдаемости регулируемых переменных. Запишем основную систему уравнений (1) в векторной форме:
где
вектор управляющих воздействий.
Электромагнитный момент m, значение которого определено из уравнения баланса мощностей, представлен посредством регулируемых переменных:
где
— модуль вектора потокосцепления статора. Для удобства анализа система вращающихся координат d, q ориентирована по току ротора irq = 0, ird = ir. Векторная диаграмма представлена на рисунке. Здесь Ψ, Ψr, i, ir — модули потокосцеплений и токов вектора состояний электрической машины; β, βr — углы, определяющие положение потокосцепления статора и ротора относительно тока ротора; μ — угол, определяет положение вектора тока статора относительно тока ротора; φ — угол, определяет положение вектора электродвижущей силы е от потокосцепления статора относительно тока статора. При пренебрежении тепловыми потерями, которые составляют 1–2% от полной мощности, cos(φ) является энергетической оценкой, характеризующей использование мощности, подводимой к обмоткам электрической машины.

Рис. Векторная диаграмма работы электрической машины
Из уравнения баланса мощностей следует, что состояние электрической машины зависит от четырех независимых переменных. В качестве таких переменных могут быть рассмотрены электромагнитный момент m, угловая скорость вращения ротора ω и два аргумента β, φ, которых достаточно для определения положения всех изображающих векторов [6]. Из приведенного числа переменных m и ω заданы условиями технологической задачи. Варьируемыми величинами являются аргументы β, φ, посредством которых осуществляется поиск энергетически желаемых режимов работы электрической машины [7].
Рассмотрим режимы электрической машины, которые могут выступать в качестве желаемых [8]. Одной из основных энергетических характеристик является коэффициент полезного действия η, величина которого зависит от мощности потерь ΔР = ITRI.
где F(β, φ) — функция энергетического состояния:
Условия, в которых работа электрической машины выполняется при абсолютном минимуме тепловых потерь, возможны только при минимуме функции (4):
и достигаются при определенном положении регулируемых переменных, которое можно характеризовать углами β, φ в области аргументов, где возможно сформировать положительный электромагнитный момент:
При росте нагрузки режим работы в условиях минимума потерь мощности связан с существенным изменением потокосцеплений и значительным ростом величины реактивной мощности. Поэтому такая энергетическая характеристика, как cosφ, играет значительную роль при выборе желаемого режима работы электрической машины. Положение изображающих векторов, при котором работа электрической машины осуществляется при минимуме энергии Wэм, накапливаемой в обмотках электрической машины, имеет определенные достоинства и определено посредством минимизации функции энергетического состояния f(β, φ):
где Wэм = 0,5ITΨ,
Минимум функции энергетического состояния (6):
достигается при другом положении изображающих векторов:
Этот режим работы позволяет минимизировать мощность, подводимую к обмоткам двигателя для формирования электромагнитного момента электрической машины в динамических процессах. Вместе с тем режим работы при минимуме энергии, накапливаемой в обмотках двигателя, осуществляется при более значительных токах и, следовательно, более высоких потерях. Существующие противоречия эффективности работы электрической машины разрешаются посредством установленной взаимосвязи между коэффициентом полезного действия η и параметром времени Тэм, характеризующим интенсивность процессов электромеханического преобразования энергии [8] в области аргументов, где возможно сформировать электромагнитный момент:
Из выражения (8) следует, задаваясь потенциально реализуемыми требованиями к энергетическим характеристикам, всегда возможно определить положение векторов, наилучшим образом сочетающее динамические и энергетические свойства работы электрической машины.
Для формирования задания регулируемых переменных в области допустимых управлений установлена зависимость вектора Ψ от модуля потокосцепления статора ψ и положения векторов в области аргументов β, φ, где возможно сформировать электромагнитный момент:
В — матрица коэффициентов, посредством аргументов β и φ отражающих положение изображающих векторов (10).
Для решения поставленной задачи на основании (9) задание для вектора регулируемых переменных Ψref представлено в зависимости не только от положения векторов, но и от электромагнитного момента (3):
Рассмотрим формирование воздействий, в области допустимого управления, обеспечивающих оптимальный по быстродействию переход системы из начального , определенное заданной величиной электромагнитного момента. Критерием оптимальности является время.
Для этой цели вектор напряжения сформирован таким образом, чтобы в совокупности с обратными связями по регулируемым переменным Ψ он отражал задание Uref выходной величины системы (1):
где K — матрица коэффициентов обратных связей, соответствующая по размерности матрице R, Тz — параметр времени, характеризующий желаемый темп изменения выходной величины системы.
Умножив левую и правую часть уравнения (2) на модуль вектора потокосцепления статора , при управлении (12), состояние электрической машины представлено в зависимости от положения векторов, заданного матрицей В, параметров обратных связей, заданных матрицей К и сигнала задания Uref электромагнитного момента:
где
Для определения элементов матриц К и В, посредством которых формируется наилучшее управление (12), посредством гамильтониана быстродействия (функции Гамильтона) установлена взаимосвязь между оптимальным управлением, регулируемыми переменными и координатами сопряженной системы. Гамильтониан быстродействия Н динамической системы (11) имеет вид:
где координаты вектора S сопряженной системы:
имеют довольно сложную зависимость во времени:
где S(0) — начальное значение координат вектора сопряженной системы.
Поскольку выходной величиной системы управления (13) является электромагнитный момент, задающим воздействием которого является сигнал Uref, условия максимума функции Гамильтона записано следующим образом:
Из выражения (17) следует, что одним из обязательных требований достижения максимума гамильтониана, независимо от величины модуля вектора потокосцепления статора Ψ, является одинаковое изменение во времени координат вектора сопряженной системы (16). Выполнение этого требования позволяет сформировать матрицу В таким образом, чтобы сумма ее коэффициентов равнялась нулю:
Это решение для обобщенной электрической машины рассмотрено в [9]. Принципу максимума могут удовлетворять несколько, в том числе бесконечно много различных форм управления. Среди всех управлений наилучшим является то, которому соответствует максимальное значение функции Гамильтона. Гамильтониан быстродействия не может быть больше единицы.
Так как критерием оптимальности является время, то оптимальное управление должно обеспечивать и наибольшую область устойчивости основной системы. Наибольшей областью устойчивости, а следовательно, и качеством управления обладают системы, описываемые апериодическим звеном первого порядка. Для удовлетворения этих требований желаемую зависимость от времени координат вектора сопряженной системы запишем следующим образом:
Решение (18) соответствует системе уравнений:
Желаемое выражение для сопряженной системы (16) может быть получено при выполнении равенства
которое достигается посредством определенного выбора элементов матрицы обратных связей К, где Е — единичная матрица размерностью матрицы V. Определенный выбор коэффициентов матрицы К при управлении (12) обеспечивает равное быстродействие контуров регулируемых переменных основной системы уравнений. При нулевых начальных условиях регулируемые переменные изменяются одновременно и c одинаковым темпом. В этих условиях положение векторов как в статических, так и в динамических режимах изменяться не будет и будет соответствовать положению, заданному матрицей В. Умножив левую и правую части уравнения (13) на матрицу ВT, преобразуем его к виду
позволяющему при равном быстродействии контуров регулируемых переменных (19) и нулевых начальных условиях получить решение основной системы уравнений:
В этих условиях решение (18) будет соответствовать сопряженной системе (16). Требования, при которых гамильтониан быстродействия равен единице, будут выполнены в том случае, если гамильтониан не будет зависеть от задающего воздействия. Выполнение этих условий возможно, если задание для основной системы уравнений связано с начальными условиями решений сопряженной системы уравнений:
Подставляя решения основной (21) и сопряженной системы уравнений (18) в функцию (14), получим значение гамильтониана в следующем виде:
Из полученного уравнения следует, что при управлении (12) и выполнении условий (19) гамильтониан быстродействия всегда равен единице. Поэтому перевод вектора состояния электрической машины из положения, соответствующего нулевым начальным условиям, в положение, соответствующее заданию электромагнитного момента, является оптимальным по быстродействию. Величина электромагнитного момента не связана с положением изображающих векторов и описывается, при оптимизации электромагнитных процессов, следующим выражением:
Задаваясь желаемым быстродействием контуров регулируемых переменных, которое характеризуется параметром времени Тz и достигается посредством определенного выбора коэффициентов матрицы обратных связей К, получим зависимость электромагнитного момента от его задания. Так как регулируемые переменные изменяются с одинаковым темпом, электромагнитный момент (22), являющийся произведением регулируемых переменных, изменяется с темпом вдвое выше. Каждому положению изображающих векторов, заданному матрицей В посредством аргументов β, φ, соответствует своя экстремаль. Существование множества экстремалей позволяет ввести дополнительные ограничения на управление при оптимизации работы электрической машины. В качестве ограничений могут выступать режимы работы, не отвечающие заданным энергетическим требованиям. Энергетические свойства работы электрической машины зависят от положения изображающих векторов. На основании (4), (6) и (8), посредством выбора коэффициентов матрицы В, могут быть выбраны энергетически желаемые режимы работы. В работе [10] представлен частный случай реализации оптимального управления синхронной машиной с электромагнитным возбуждением, обеспечивающий наиболее быстрое формирование электромагнитного момента при минимизации тепловых потерь, в условиях минимума реактивной мощности.
Вывод
Показано, что оптимальное по быстродействию управление электрической машиной должно осуществляться при одновременном регулировании с одинаковым темпом задаваемых переменных, что достигается путем синтеза управляющих воздействий. Энергетические свойства работы электрической машины зависят от положения изображающих векторов. Формирование энергетически желаемых режимов работы электрической машины осуществляется посредством функций энергетического состояния путем выбора аргументов управляющих воздействий, отражающих положение изображающих векторов и отвечающих желаемым энергетическим требованиям. Это ключевое положение справедливо для управляющих воздействий не только при оптимизации по быстродействию, но и при многокритериальной оптимизации работы машины переменного тока, обеспечивающей наилучшее сочетание энергетических и динамических свойств электропривода.
- Blaschke F. Das Prinzip der Feldorientierung die Grundlage fur die Transvektor – Regelung von Drehfeldmashinen // Siemens Zeitschift. 1971.
- Красовский А. А. Справочник по теории автоматического управления. М.: Наука. 1987.
- Филюшов Ю. П. Метод оптимального синтеза управляющих воздействий машины переменного тока // Электротехника. 2012. № 8.
- Петров Ю. П. Вариационные методы теории оптимального управления. Л.: Энергия. 1965.
- Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Математическая теория оптимальных процессов. М.: Наука. 1976.
- Филюшов Ю. П. Оптимизация электромагнитных процессов в асинхронной короткозамкнутой машине // Электричество. 2011. № 5.
- Филюшов Ю. П. Состояние и оценки качества работы электропривода переменного тока // Силовая электроника. 2013. № 1.
- Bochencov B., Filushov Y. The Optimization of the work of the electric drive alternating current on vector criterion quality // IEEE: Strategic Technologies. IFOST 2008.
- Филюшов Ю. П. Оптимальное по быстродействию управление машиной переменного тока // Электричество. 2011. № 2.
- Пат. 2092967 (РФ) Н 02 Р 21/00. Электропривод с синхронным двигателем / Ю. П. Филюшов. // Бюл. 1997. № 28.

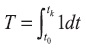







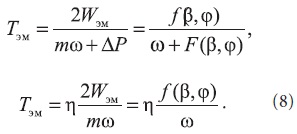

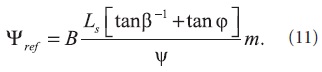
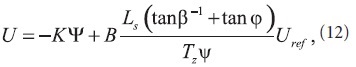








 17 мая, 2011
17 мая, 2011 15 июля, 2023
15 июля, 2023